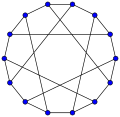
mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood. The graph is cubic, and...

In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on...

Heawood graph, the complete graph K7 (and hence K5 and K6), the Petersen graph (and hence the complete bipartite graph K3,3, since the Petersen graph...

particular graph is a connected cubic graph (regular of degree 3), has girth 6 and each part contains 7 vertices. It is the Heawood graph, the unique...

The Heawood graph is the Levi graph of the Fano plane. It is also known as the (3,6)-cage, and is 3-regular with 14 vertices. The Möbius–Kantor graph is...

smallest 2-crossing cubic graph is the Petersen graph, with 10 vertices. The smallest 3-crossing cubic graph is the Heawood graph, with 14 vertices. The...

refer to an incidence graph of any incidence structure. The Levi graph of the Fano plane is the Heawood graph. Since the Heawood graph is connected and vertex-transitive...

In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets...

In graph theory the term Heawood family refers to either one of the following two related graph families generated via ΔY- and YΔ-transformations: the...

generalization of this problem by Tait, Heawood, Ramsey and Hadwiger led to the study of the colorings of the graphs embedded on surfaces with arbitrary genus...

the complete bipartite graphs Kn,n with girth four, the Heawood graph with degree 3 and girth 6, and the Tutte–Coxeter graph with degree 3 and girth...

the Heawood number of a surface is an upper bound for the number of colors that suffice to color any graph embedded in the surface. In 1890 Heawood proved...

10-cage, the Harries graph and the Harries–Wong graph. The Petersen graph has a girth of 5 The Heawood graph has a girth of 6 The McGee graph has a girth of...

British mathematician Heawood conjecture Heawood graph Heawood number Heywood (surname) This page lists people with the surname Heawood. If an internal link...

Percy John Heawood (8 September 1861 – 24 January 1955) was a British mathematician, who concentrated on graph colouring. He was the son of the Rev. John...

In graph theory, graph coloring is a methodic assignment of labels traditionally called "colors" to elements of a graph. The assignment is subject to certain...

mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each...

3-regular graphs. Every strongly regular graph is symmetric, but not vice versa. Heawood graph Möbius–Kantor graph Pappus graph Desargues graph Nauru graph Coxeter...

In topological graph theory, an embedding (also spelled imbedding) of a graph G {\displaystyle G} on a surface Σ {\displaystyle \Sigma } is a representation...

individual graphs are cubic and symmetric, including the utility graph, the Petersen graph, the Heawood graph, the Möbius–Kantor graph, the Pappus graph, the...

Coxeter graph may also be constructed from the smaller distance-regular Heawood graph by constructing a vertex for each 6-cycle in the Heawood graph and an...

instance, the Heawood graph has crossing number 3, but it is not necessary for its three crossings to all occur on the same edge of the graph, so it is 1-planar...

graphs include the Petersen graph, the Heawood graph, the wheel graph W 7 {\displaystyle W_{7}} (the only wheel graph that is a unit distance graph)...

In the mathematical field of graph theory, a graph G is symmetric or arc-transitive if, given any two ordered pairs of adjacent vertices ( u 1 , v 1 )...

subgraphs of the Dejter graph can be presented as covering graphs of the Heawood graph, namely as 8-covers of the Heawood graph. This is suggested in each...

graphs (such as the Petersen graph, the Heawood graph and the vertices and edges of the Platonic solids). The finite Cayley graphs (such as cube-connected...

the Heawood conjecture on the number of colors needed when a two-dimensional surface is partitioned into cells by a graph embedding. The Heawood conjecture...

Thomas (1998), p. 848. Heawood (1890). Tait (1880). Hadwiger (1943). Wilson (2014), pp. 139–142. Gary Chartrand and Linda Lesniak, Graphs & Digraphs (CRC Press...

Tetrahedral graph), K3,3, the Petersen graph, the Cubical graph, the Heawood graph, the Pappus graph, the Coxeter graph, the Tutte–Coxeter graph, the Dodecahedral...

of each vertex is given by the corresponding Cayley graph, so is just the bipartite Heawood graph, i.e. exactly the same as in the affine building for...