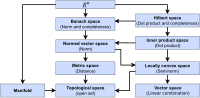
In mathematics, a homogeneous space is, very informally, a space that looks the same everywhere, as you move through it, with movement given by the action...

In mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G in which the stabilizer subgroup of every point...

variety (or simply flag variety) is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real...

codomain are vector spaces over a field F: a function f : V → W {\displaystyle f:V\to W} between two F-vector spaces is homogeneous of degree k {\displaystyle...

symmetry on a space, where the symmetries of the space were transformations forming a Lie group. The geometries of interest were homogeneous spaces G/H, but...

projective space being considered. For example, two homogeneous coordinates are required to specify a point on the projective line and three homogeneous coordinates...

function defined by a homogeneous polynomial. A binary form is a form in two variables. A form is also a function defined on a vector space, which may be expressed...

{\displaystyle k} -frames) are still homogeneous spaces for the orthogonal group, but not principal homogeneous spaces: any k {\displaystyle k} -frame can...

F n ) {\displaystyle V_{k}(\mathbb {F} ^{n})} can be viewed as a homogeneous space for the action of a classical group in a natural manner. Every orthogonal...

Thus any symmetric space is a reductive homogeneous space, but there are many reductive homogeneous spaces which are not symmetric spaces. The key feature...

system. The displacement vectors for that affine space are the solutions of the corresponding homogeneous linear system, which is a linear subspace. Linear...

symplectic vector space V. Its dimension is 1/2n(n + 1) (where the dimension of V is 2n). It may be identified with the homogeneous space U(n)/O(n), where...

deeper and more general). In other words, the "traditional spaces" are homogeneous spaces; but not for a uniquely determined group. Changing the group...

Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's Elements, it was the three-dimensional...

space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to −1. It is homogeneous...

of Leibniz Homogeneous space for a Lie group G, or more general transformation group Homogeneous function Homogeneous polynomial Homogeneous equation (linear...

{\mathcal {H}}} . Thus, anti-de Sitter is a reductive homogeneous space, and a non-Riemannian symmetric space. A d S n {\displaystyle \mathrm {AdS} _{n}} is...

basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space. In lay terms, a frame...

(orthonormal k-frames) are still homogeneous spaces for the orthogonal group, but not principal homogeneous spaces: any k-frame can be taken to any other...

The geometry of a n-dimensional space can also be described with Riemannian geometry. An isotropic and homogeneous space can be described by the metric:...

the dual space, a homogeneous space for SU(2) and SL(2,C). Irreducible compact Hermitian symmetric spaces are exactly the homogeneous spaces of simple...

group G {\displaystyle G} is given, so that each fiber is a principal homogeneous space. The bundle is often specified along with the group by referring to...

giving the Grassmannian a geometric structure is to express it as a homogeneous space. First, recall that the general linear group G L ( V ) {\displaystyle...

timelike vector, so the homogeneous space SO+(1, 3) / SO(3) is the momentum space of a massive particle; geometrically, this space is none other than three-dimensional...

even-dimensional ones cannot. Complex projective space is a special case of a Grassmannian, and is a homogeneous space for various Lie groups. It is a Kähler manifold...

Function space G-space Geometric space Green space (topological space) Hardy space Hausdorff space Heisenberg space Hilbert space Homogeneous space Inner...

vector space. For a given n the elements of V n {\displaystyle V_{n}} are then called homogeneous elements of degree n. Graded vector spaces are common...

Cartan connections describe the geometry of manifolds modelled on homogeneous spaces. The theory of Cartan connections was developed by Élie Cartan, as...

set. Examples include quotient spaces in linear algebra, quotient spaces in topology, quotient groups, homogeneous spaces, quotient rings, quotient monoids...

for homogeneous mixture and "non-uniform mixture" is another term for heterogeneous mixture. These terms are derived from the idea that a homogeneous mixture...