integral calculus, Euler's formula for complex numbers may be used to evaluate integrals involving trigonometric functions. Using Euler's formula, any trigonometric...

Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric...

been given simple yet ambiguous names such as Euler's function, Euler's equation, and Euler's formula. Euler's work touched upon so many fields that he is...

mathematics, the Euler–Maclaurin formula is a formula for the difference between an integral and a closely related sum. It can be used to approximate integrals...

and is known as the Euler integral of the second kind. (Euler's integral of the first kind is the beta function.) Using integration by parts, one sees...

logarithm, also commonly written as ln(x) or loge(x). Euler's constant (sometimes called the Euler–Mascheroni constant) is a mathematical constant, usually...

differencePages displaying wikidata descriptions as a fallback Integration using Euler's formula – Use of complex numbers to evaluate integrals Liouville's theorem...

has Euler characteristic 2. This viewpoint is implicit in Cauchy's proof of Euler's formula given below. There are many proofs of Euler's formula. One...

numerical integration of ordinary differential equations and is the simplest Runge–Kutta method. The Euler method is named after Leonhard Euler, who first...

Verlet integration (French pronunciation: [vɛʁˈlɛ]) is a numerical method used to integrate Newton's equations of motion. It is frequently used to calculate...

learning resources about Integration by Substitution Integration by substitution at Encyclopedia of Mathematics Area formula at Encyclopedia of Mathematics...

introduced scientific notation. He discovered what is now known as Euler's formula, that for any real number φ {\displaystyle \varphi } , the complex...

arise in probability theory. The term Lebesgue integration can mean either the general theory of integration of a function with respect to a general measure...

into an integral by means of the Abel–Plana formula and evaluated using techniques for numerical integration. If the series is truncated at the right time...

using Pick's theorem (proved in a different way) as the basis for a proof of Euler's formula. Alternative proofs of Pick's theorem that do not use Euler's...

expression that a differential equation is multiplied by to facilitate integration. For example, the nonlinear second order equation d 2 y d t 2 = A y 2...

{d}}x=n\ln n-n+1,} and the error in this approximation is given by the Euler–Maclaurin formula: ln ⁡ ( n ! ) − 1 2 ln ⁡ n = 1 2 ln ⁡ 1 + ln ⁡ 2 + ln ⁡ 3 + ⋯ +...

{1}{1-p^{-s}}}\cdots } Both sides of the Euler product formula converge for Re(s) > 1. The proof of Euler's identity uses only the formula for the geometric series and...

used to find numerical approximations to the solutions of ordinary differential equations (ODEs). Their use is also known as "numerical integration"...

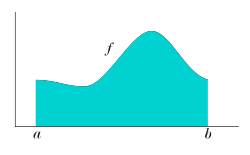
theorem of calculus or approximated by numerical integration, or simulated using Monte Carlo integration. Imagine you have a curve on a graph, and the curve...

infinite Euler product for π. Wallis sieve The Pippenger product formula obtains e by taking roots of terms in the Wallis product. "Wallis Formula". "Integrating...

calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of...

infinite series. Of course, Euler's original reasoning requires justification (100 years later, Karl Weierstrass proved that Euler's representation of the sine...

be done readily on the power series representation; for instance, Euler's formula follows from Taylor series expansions for trigonometric and exponential...

e^{-x^{2}}\,dx\right)^{2};} on the other hand, by shell integration (a case of double integration in polar coordinates), its integral is computed to be...

In mathematics, an Euler–Cauchy equation, or Cauchy–Euler equation, or simply Euler's equation, is a linear homogeneous ordinary differential equation...

complex analysis, "differentiation is equivalent to integration": complex differentiation, like integration, behaves well under uniform limits – a result that...

by using above formulas, and then using the identity e a + b = e a e b {\displaystyle e^{a+b}=e^{a}e^{b}} for simplifying the result. Euler's formula can...

of integration is one of the earliest used. The reduction formula can be derived using any of the common methods of integration, like integration by substitution...

by symbolic integration, thus avoiding numerical integration. The fundamental theorem of calculus relates differentiation and integration, showing that...