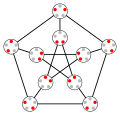
In graph theory, the Kneser graph K(n, k) (alternatively KGn,k) is the graph whose vertices correspond to the k-element subsets of a set of n elements...

tropical curves. The Petersen graph is the complement of the line graph of K 5 {\displaystyle K_{5}} . It is also the Kneser graph K G 5 , 2 {\displaystyle...

linear graphs. Certain Kneser graphs, and certain strongly regular graphs, are also locally linear. The question of how many edges locally linear graphs can...

Odd chords are used to define strongly chordal graphs. 5.  An odd graph is a special case of a Kneser graph, having one vertex for each (n − 1)-element subset...

Approximation in algebraic groups Betke–Kneser theorem Kneser–Tits conjecture Kneser's theorem (combinatorics) Kneser graphs "Einfach zusammenhängende algebraische...

each point. The Desargues graph can also be viewed as the generalized Petersen graph G(10,3) or the bipartite Kneser graph with parameters 5,2. It is...

norm 1 vector then the two even lattices are isomorphic.) The Kneser neighborhood graph in 8n dimensions has a point for each even lattice, and a line...

by a pair of vertices and each Petersen graph edge by a pair of crossed edges. It is the bipartite Kneser graph H5,2. Its vertices can be labeled by the...

{\displaystyle J(n,2)} is the line graph of Kn and the complement of the Kneser graph K ( n , 2 ) . {\displaystyle K(n,2).} J ( n , k ) {\displaystyle J(n...

subgraphs Shift graph, a family of triangle-free graphs with arbitrarily high chromatic number The Kneser graph K G 3 k − 1 , k {\displaystyle KG_{3k-1,k}}...

The theorem may also be formulated in terms of graph theory: the independence number of the Kneser graph K G n , r {\displaystyle KG_{n,r}} for n ≥ 2 r...

as the triangular graph, the Johnson graph J(n, 2), or the complement of the Kneser graph KGn,2. Triangular graphs are characterized by their spectra,...

complete graphs, refining the usual notion of colorings. Fractional and b-fold coloring can be defined using homomorphisms into Kneser graphs. T-colorings...

in the second, so this bipartite graph is not complete. It is an example of both crown graph and bipartite Kneser graph. An object illuminated by parallel...

sets in Kneser graphs), these are the unique maximum independent sets in this graph. It is one of seven known triangle-free strongly regular graphs. Its...

complete graph, as the tensor product Kn × K2, as the complement of the Cartesian direct product of Kn and K2, or as a bipartite Kneser graph Hn,1 representing...

} Mathematics portal Binomial coefficient Combinatorics Block design Kneser graph List of permutation topics Multiset Probability Reichl, Linda E. (2016)...

orientability of triangle-free graphs, arXiv:2003.06204v1. S. Kitaev and A. Saito. On semi-transitive orientability of Kneser graphs and their complements, Discrete...

available colors. Equivalently, it can be defined as a homomorphism to the Kneser graph KGa,b. The b-fold chromatic number χ b ( G ) {\displaystyle \chi _{b}(G)}...

combinatorics developed by László Lovász to compute the chromatic number of Kneser graphs. The triangle-free property is then strengthened as follows: if one...

corresponding subsets are disjoint. That is, O n {\displaystyle O_{n}} is the Kneser graph K G ( 2 n − 1 , n − 1 ) {\displaystyle KG(2n-1,n-1)} . O 2 {\displaystyle...

Coxeter graph. (See image.) This construction exhibits the Coxeter graph as an induced subgraph of the odd graph O4, also known as the Kneser graph KG7,3...

Turán's theorem Shannon capacity and Lovász number Chromatic number of Kneser graphs Friendship theorem Some proofs using the probabilistic method Klarreich...

no-three-in-line problem, and a geometric proof of the chromatic number of Kneser graphs. Every hyperplane intersects the moment curve in a finite set of at...

Academy of Sciences from 2014 to 2020. In graph theory, Lovász's notable contributions include the proofs of Kneser's conjecture and the Lovász local lemma...

1955 conjecture by Martin Kneser, according to which the Kneser graphs K G 2 n + k , n {\displaystyle KG_{2n+k,n}} have no graph coloring with k + 1 {\displaystyle...

uses a Kneser graph. Let k := ⌊ m + n 2 ⌋ {\displaystyle k:={\bigg \lfloor }{\frac {m+n}{2}}{\bigg \rfloor }} , and let G be the Kneser graph K G ( m...

In graph theory, the Lovász number of a graph is a real number that is an upper bound on the Shannon capacity of the graph. It is also known as Lovász...

is a Mexican mathematician specializing in graph theory, including work on graph coloring, Kneser graphs, cages, and finite geometry. She is a researcher...

His name is known in graph theory mainly for Tait's conjecture on cubic graphs. He is also one of the namesakes of the Tait–Kneser theorem on osculating...