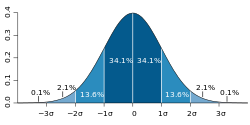
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. While...

Cramér's theorem is a fundamental result in the theory of large deviations, a subdiscipline of probability theory. It determines the rate function of a series...

In mathematics, Laplace's principle is a basic theorem in large deviations theory which is similar to Varadhan's lemma. It gives an asymptotic expression...

mathematics — specifically, in large deviations theory — the contraction principle is a theorem that states how a large deviation principle on one space "pushes...

large deviations theory — a rate function is a function used to quantify the probabilities of rare events. Such functions are used to formulate large...

In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts...

divergence Le Cam's theorem Large deviations theory Contraction principle (large deviations theory) Varadhan's lemma Tilted large deviation principle Rate function...

Law of large numbers Law of the iterated logarithm Slutsky's theorem Delta method Asymptotic analysis Exact statistics Large deviations theory Höpfner...

the Contraction principle in large deviations theory reduces Freidlin–Wentzell's problem to demonstrating the large deviation principle for ( t , ε B t )...

In mathematics, Varadhan's lemma is a result from the large deviations theory named after S. R. Srinivasa Varadhan. The result gives information on the...

variance is the average of the squared deviations from the mean.) A useful property of the standard deviation is that, unlike the variance, it is expressed...

^{n}} to functional Wiener integration. The theorem is used in the large deviations theory of stochastic processes. Roughly speaking, out of Schilder's theorem...

to Mark Freidlin and Alexander D. Wentzell) is a result in the large deviations theory of stochastic processes. Roughly speaking, the Freidlin–Wentzell...

Fisher–Tippett–Gnedenko theorem Generalized extreme value distribution Large deviation theory Outlier Pareto distribution Pickands–Balkema–de Haan theorem Rare...

distribution Laplace principle (large deviations theory) LaplacesDemon – software Large deviations theory Large deviations of Gaussian random functions LARS...

a German xDT format to transfer laboratory tests Large deviations theory, field of probability theory Learning Design and Technology, an academic program...

{\displaystyle a} and b . {\displaystyle b.} This estimate is useful in large deviations theory under exponential moment conditions, because b ln ⁡ b {\displaystyle...

has been suppressed by assuming that the variable has been measured as deviations from its mean) as X t = 1 ϕ ( B ) ε t . {\displaystyle X_{t}={\frac {1}{\phi...

number of samples. Such results are studied in large deviations theory; intuitively, it is the large deviations that would violate equipartition, but these...

distribution. In the language of large deviations theory, Sanov's theorem identifies the rate function for large deviations of the empirical measure of a...

specifically, in large deviations theory — the tilted large deviation principle is a result that allows one to generate a new large deviation principle from...

the concept of Gromov–Hausdorff limits is closely related to large-deviations theory. Intrinsic flat distance David A. Edwards, "The Structure of Superspace"...

tests are computed using Sanov's theorem and other results from large deviations theory. Consider a binary hypothesis testing problem in which observations...

stationary phase Method of steepest descent Large deviations theory Laplace principle (large deviations theory) Laplace's approximation Tierney, Luke; Kadane...

statistics and probabilistic number theory. John Kingman described him as "one of the giants of statistical theory". Harald Cramér was born in Stockholm...

In probability theory and statistics, diffusion processes are a class of continuous-time Markov process with almost surely continuous sample paths. Diffusion...

that the deviations in real GNP are comparatively small and might be attributable to measurement errors rather than real deviations. We call large positive...

implement in computer code, and lends itself well to risk management of large portfolios of options in real time. It is convenient to express the solution...

L-theory the K-theory of quadratic forms. Large deviations theory part of probability theory studying events of small probability (tail events). Large sample...

is a result in large deviations theory. Heuristically speaking, the Dawson–Gärtner theorem allows one to transport a large deviation principle on a “smaller”...