In mathematics, the Legendre chi function is a special function whose Taylor series is also a Dirichlet series, given by χ ν ( z ) = ∑ k = 0 ∞ z 2 k +...
3 KB (566 words) - 10:44, 15 June 2025
Taylor series (section Exponential function)
_{n=1}^{\infty }{\frac {1}{n^{3}}}x^{n}\end{aligned}}} The Legendre chi functions are defined as follows: χ 2 ( x ) = ∑ n = 0 ∞ 1 ( 2 n + 1 ) 2 x...
48 KB (8,229 words) - 17:42, 2 July 2025
Dirichlet beta function Dirichlet L-function Hurwitz zeta function Legendre chi function Lerch transcendent Polylogarithm and related functions: Incomplete...
10 KB (1,065 words) - 19:46, 12 July 2025
the Legendre chi function χ ν {\displaystyle \chi _{\nu }} as C ν ( x ) = Re χ ν ( e i x ) {\displaystyle C_{\nu }(x)=\operatorname {Re} \,\chi _{\nu...
22 KB (4,190 words) - 03:21, 20 July 2025
other series for the zeta-function-related cases of the Legendre chi function, the polygamma function, and the Riemann zeta function include χ 1 ( z ) = ∑...
62 KB (11,140 words) - 00:12, 16 July 2025
Polylogarithm (redirect from De Jonquière's function)
{\operatorname {Ti} _{n}(t)}{t}}dt,} which explains the function name. The Legendre chi function χs(z) (Lewin 1958, Ch. VII § 1.1; Boersma & Dempsey 1992)...
60 KB (10,143 words) - 06:23, 7 July 2025
Gauss–Legendre algorithm Gauss–Legendre method Gauss–Legendre quadrature Legendre (crater) Legendre chi function Legendre duplication formula Legendre–Papoulis...
1 KB (111 words) - 16:48, 20 March 2022
Inverse tangent integral (category Special functions)
Dirichlet beta function. The inverse tangent integral is related to the Legendre chi function χ 2 ( x ) = x + x 3 3 2 + x 5 5 2 + ⋯ {\textstyle \chi _{2}(x)=x+{\frac...
5 KB (911 words) - 19:39, 12 February 2024
distribution with three degrees of freedom). The probability density function (pdf) of the chi-distribution is f ( x ; k ) = { x k − 1 e − x 2 / 2 2 k / 2 −...
10 KB (1,726 words) - 21:53, 23 November 2024
1 2 ( χ ) {\displaystyle Q_{m-{\frac {1}{2}}}(\chi )} is the odd-half-integer degree Legendre function of the second kind, which is a toroidal harmonic...
11 KB (1,910 words) - 01:17, 15 August 2024
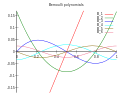
Bernoulli polynomials (redirect from Bernoulli function)
}(x)&=S_{\nu }(1-x).\end{aligned}}} They are related to the Legendre chi function χ ν {\displaystyle \chi _{\nu }} as C ν ( x ) = Re χ ν ( e i x ) S ν ( x )...
19 KB (4,342 words) - 18:27, 2 June 2025
Stickelberger's theorem. When χ is the Legendre symbol, J ( χ , χ ) = − χ ( − 1 ) = ( − 1 ) p + 1 2 . {\displaystyle J(\chi ,\chi )=-\chi (-1)=(-1)^{\frac {p+1}{2}}\...
4 KB (551 words) - 19:07, 3 May 2025
Lerch transcendent (redirect from Hurwitz-Lerch zeta function)
{\tfrac {1}{2}})} The Legendre chi function: χ s ( z ) = ∑ k = 0 ∞ z 2 k + 1 ( 2 k + 1 ) s = z 2 s Φ ( z 2 , s , 1 2 ) {\displaystyle \chi _{s}(z)=\sum _{k=0}^{\infty...
17 KB (3,654 words) - 17:40, 28 May 2025
Dirichlet character (category Zeta and L-functions)
related branches of mathematics, a complex-valued arithmetic function χ : Z → C {\displaystyle \chi :\mathbb {Z} \rightarrow \mathbb {C} } is a Dirichlet character...
51 KB (11,916 words) - 20:16, 15 June 2025
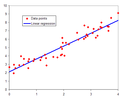
Regression analysis (redirect from Regression function)
time. The method of least squares was published by Legendre in 1805, and by Gauss in 1809. Legendre and Gauss both applied the method to the problem of...
37 KB (5,235 words) - 03:23, 20 June 2025
Quadratic reciprocity (section Legendre's version)
product of the Riemann zeta function and a certain Dirichlet L-function The Jacobi symbol is a generalization of the Legendre symbol; the main difference...
111 KB (8,574 words) - 05:56, 18 July 2025
theory, an arithmetic, arithmetical, or number-theoretic function is generally any function whose domain is the set of positive integers and whose range...
53 KB (7,555 words) - 01:12, 6 April 2025
{\displaystyle G(\chi )=\mu \left({\frac {N}{N_{0}}}\right)\chi _{0}\left({\frac {N}{N_{0}}}\right)G\left(\chi _{0}\right)} where μ is the Möbius function. Consequently...
7 KB (918 words) - 18:21, 8 June 2023
parameters and the observed data. The method was first proposed by Adrien-Marie Legendre in 1805 and further developed by Carl Friedrich Gauss. The method of least...
36 KB (5,243 words) - 23:15, 19 June 2025
Semi-continuity (redirect from Semi-continuous function)
convex function. Some operations in convex analysis, such as the Legendre transform automatically produce closed convex functions. The Legendre transform...
40 KB (6,634 words) - 19:26, 19 July 2025
Wigner D-matrix (redirect from Wigner D-function)
index equal to zero are proportional to spherical harmonics and associated Legendre polynomials, normalized to unity and with Condon and Shortley phase convention:...
21 KB (4,744 words) - 07:55, 17 June 2025
Vooren. Boersma, J.; Dempsey, J.P. (1992). "On the evaluation of Legendre's chi-function" (PDF). Mathematics of Computation. 59 (199): 157–163. doi:10.2307/2152987...
2 KB (99 words) - 02:32, 21 November 2024
( a ) ζ a {\displaystyle \sum \chi (a)\zeta ^{a}} where χ ( a ) {\displaystyle \chi (a)} here stands for the Legendre symbol (a/p), and the sum is taken...
7 KB (1,130 words) - 03:22, 28 March 2021
extension of the domain is necessary for defining L functions. See Legendre symbol#Properties of the Legendre symbol for examples Lemmermeyer, pp 111–end Davenport...
54 KB (5,575 words) - 07:28, 20 July 2025
F(n)=n(n+1)} and χ a Legendre symbol. Here the sum can be evaluated (as −1), a result that is connected to the local zeta-function of a conic section....
5 KB (710 words) - 09:54, 2 March 2025
Practice. Boca Raton: CRC Press. p. 204. ISBN 9781584886167. Legendre, Pierre; Legendre, Louis (2012). Numerical Ecology. Amsterdam: Elsevier. p. 465...
22 KB (3,230 words) - 07:08, 27 December 2024
continued-fraction representation of the tangent function. French mathematician Adrien-Marie Legendre proved in 1794 that π2 is also irrational. In 1882...
148 KB (17,240 words) - 14:14, 14 July 2025
\zeta _{p}=\exp(2\pi i/p)} . Equivalently, we can write this using the Legendre symbol as g ( a ; p ) = ∑ n = 0 p − 1 ( 1 + ( n p ) ) ζ p a n . {\displaystyle...
8 KB (1,669 words) - 20:56, 16 July 2025
dynamics and cost functions DNSS point — initial state for certain optimal control problems with multiple optimal solutions Legendre–Clebsch condition...
70 KB (8,327 words) - 09:12, 7 June 2025
Integration by parts (section Gamma function identity)
corresponding to the function of bounded variation χ [ a , b ] ( x ) f ( x ) {\displaystyle \chi _{[a,b]}(x)f(x)} , and functions f ~ , φ ~ {\displaystyle...
37 KB (7,162 words) - 00:16, 22 July 2025