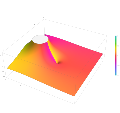
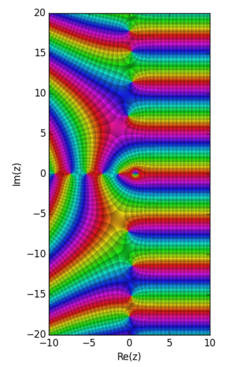
In mathematics, the Lerch transcendent, is a special function that generalizes the Hurwitz zeta function and the polylogarithm. It is named after Czech...

Cls(θ) can be chosen as the real or imaginary part of Lis(eiθ). The Lerch transcendent is given by Φ ( z , s , q ) = ∑ k = 0 ∞ z k ( k + q ) s {\displaystyle...

Dirichlet L-function Hurwitz zeta function Legendre chi function Lerch transcendent Polylogarithm and related functions: Incomplete polylogarithm Clausen...

terms of the other — and both functions are special cases of the Lerch transcendent. Polylogarithms should not be confused with polylogarithmic functions...

coach Gustov C. Lerch House Lerch Bates Lerch transcendent Lorch (disambiguation) Blub This page lists people with the surname Lerch. If an internal link...

The inverse tangent integral can also be written in terms of the Lerch transcendent Φ ( z , s , a ) = ∑ n = 0 ∞ z n ( n + a ) s : {\textstyle \Phi (z...

those articles. The Legendre chi function is a special case of the Lerch transcendent, and is given by χ ν ( z ) = 2 − ν z Φ ( z 2 , ν , 1 / 2 ) . {\displaystyle...

Kν are the corresponding modified Bessel functions, and Φ is the Lerch transcendent. Gradshteyn and Ryzhik Andrews, L. C. (1985). Special Functions for...

products for some classical constants via analytic continuations of Lerch's transcendent". The Ramanujan Journal. 16 (3): 247–270. arXiv:math.NT/0506319....

}{(k+z)^{n+1}}}\right)} Where δn0 is the Kronecker delta. Also the Lerch transcendent Φ ( − 1 , m + 1 , z ) = ∑ k = 0 ∞ ( − 1 ) k ( z + k ) m + 1 {\displaystyle...

The Barnes zeta function generalizes the Hurwitz zeta function. The Lerch transcendent generalizes the Hurwitz zeta: Φ ( z , s , q ) = ∑ k = 0 ∞ z k ( k...

4}\right)\right).} Another equivalent definition, in terms of the Lerch transcendent, is: β ( s ) = 2 − s Φ ( − 1 , s , 1 2 ) , {\displaystyle \beta (s)=2^{-s}\Phi...

{1+{\sqrt {2}}}{2\left(2-{\sqrt {2}}\right)}}\right).} If one defines the Lerch transcendent Φ(z,s,α) by Φ ( z , s , α ) = ∑ n = 0 ∞ z n ( n + α ) s , {\displaystyle...

and Sondow give a representation in terms of the derivative of the Lerch transcendent Φ ( z , s , q ) {\displaystyle \Phi (z,s,q)} : ln ⁡ σ = − 1 2 ∂ Φ...

products for some classical constants via analytic continuations of Lerch's transcendent, Ramanujan Journal 16 (2008), 247–270. H. J. Brothers and J. A. Knox...

and generalizations. Further generalization comes from use of the Lerch transcendent: ∑ x z x ( x + a ) s = − z x Φ ( z , s , x + a ) + C {\displaystyle...

}}z=1\end{cases}}\end{aligned}}} where Φ ( ) {\displaystyle \Phi ()} is the Lerch transcendent function and coth() is the hyperbolic cotangent function. In terms...

^{2}}}-{\frac {13}{4}}} A {\displaystyle A} also is related to the Lerch transcendent: ∂ Φ ∂ s ( − 1 , − 1 , 1 ) = 3 ln ⁡ A − 1 3 ln ⁡ 2 − 1 4 {\displaystyle...

}}z=1\end{cases}}\end{aligned}}} where Φ ( ) {\displaystyle \Phi ()} is the Lerch transcendent function. In terms of the circular variable z = e i θ {\displaystyle...

products for some classical constants via analytic continuations of Lerch's transcendent". The Ramanujan Journal. 16 (3): 247–270. arXiv:math/0506319. doi:10...

transformations defined above is related to more Hurwitz-zeta-like, or Lerch-transcendent-like, generating functions. Specifically, if we define the even more...