In mathematics, a Lipschitz domain (or domain with Lipschitz boundary) is a domain in Euclidean space whose boundary is "sufficiently regular" in the sense...

Cauchy–Lipschitz theorem Lipschitz domain Lipschitz quaternion Lipschitz continuity Uniform, Hölder and Lipschitz continuity Lipschitz distance Lipschitz-continuous...

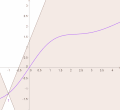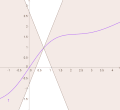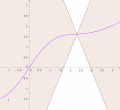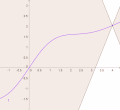
In mathematical analysis, Lipschitz continuity, named after German mathematician Rudolf Lipschitz, is a strong form of uniform continuity for functions...

injection and surjection Codomain Domain decomposition Effective domain Endofunction Image (mathematics) Lipschitz domain Naive set theory Range of a function...

considered types of domains are domains with continuous boundary, Lipschitz boundary, C1 boundary, and so forth. A bounded domain is a domain that is bounded...

space R n {\displaystyle \mathbb {R} ^{n}} with a Lipschitz boundary (i.e., Ω is a Lipschitz domain). Then there exists a constant C, depending only on...

of strong derivatives). Suppose Ω is a bounded, simply-connected, Lipschitz domain. Every square-integrable vector field u ∈ (L2(Ω))3 has an orthogonal...

periodicity. The class of Lipschitz groups (a.k.a. Clifford groups or Clifford–Lipschitz groups) was discovered by Rudolf Lipschitz. In this section we assume...

version) of the trace theorem for Lipschitz domains can be found in Gagliardo. On a C 1 {\textstyle C^{1}} -domain, the trace operator can be defined...

{R} ^{n}} is either the full space, a half-space or a bounded and Lipschitz domain. If s ∈ ( 0 , 1 ) {\displaystyle s\in (0,1)} and p ≥ 1 {\displaystyle...

as interpolation inequalities. Let Ω {\displaystyle \Omega } be a Lipschitz domain in R n {\displaystyle \mathbb {R} ^{n}} for n = 2  or  3 {\displaystyle...

Hurwitz (1919). A Lipschitz quaternion (or Lipschitz integer) is a quaternion whose components are all integers. The set of all Lipschitz quaternions L =...

and K is a simply connected Lipschitz domain, so that the integral of f vanishes on every congruent copy of K. Then the domain is a ball. A special case...

Cauchy–Lipschitz theorem, or the existence and uniqueness theorem. The theorem is named after Émile Picard, Ernst Lindelöf, Rudolf Lipschitz and Augustin-Louis...

theorem and Kondrashov the Lp theorem. Let Ω ⊆ Rn be an open, bounded Lipschitz domain, and let 1 ≤ p < n. Set p ∗ := n p n − p . {\displaystyle p^{*}:={\frac...

by the Rellich–Kondrachov theorem: let Ω ⊆ Rn be an open, bounded, Lipschitz domain, and let 1 ≤ p < n. Set p ∗ = n p n − p . {\displaystyle p^{*}={\frac...

If D ⊂ R n {\displaystyle D\subset \mathbb {R} ^{n}} is a bounded Lipschitz domain, then harmonic measure and (n − 1)-dimensional Hausdorff measure are...

"Hodge–Dirac, Hodge–Laplacian and Hodge–Stokes operators in $L^p$ spaces on Lipschitz domains". Revista Matemática Iberoamericana. 34 (4): 1711–1753. arXiv:1608...

→ H 2 {\displaystyle f:U\rightarrow H_{2}} is a Lipschitz-continuous map, then there is a Lipschitz-continuous map F : H 1 → H 2 {\displaystyle F:H_{1}\rightarrow...

noncommutative domain. More generally, any division ring is a domain, since every nonzero element is invertible. The set of all Lipschitz quaternions, that...

;\\u(x)=0,&x\in \partial \Omega ;\end{cases}}} where Ω is a bounded Lipschitz domain in Rn. The corresponding weak form of the problem is to find u in the...

the k-Lipschitz functions, the moduli ω(t) := ktα describe the Hölder continuity, the modulus ω(t) := kt(|log t|+1) describes the almost Lipschitz class...

Mathematics Institutions University of Chicago Thesis Hp spaces on Lipschitz domains (1978) Doctoral advisor Alberto Calderón Doctoral students Donatella...

zero angle at the tip are excluded. Lipschitz domains are reasonable enough, which includes convex domains and domains with continuously differentiable boundary...

PDE in divergence form: Assume that the domain Ω {\displaystyle \Omega } is a bounded connected Lipschitz domain whose boundary consists of a finite number...

is constant (see proof below). If α = 1, then the function satisfies a Lipschitz condition. For any α > 0, the condition implies the function is uniformly...

mathematical analysis, including balls, completeness, as well as uniform, Lipschitz, and Hölder continuity, can be defined in the setting of metric spaces...

algebras, Fourier theory, singular integrals, and harmonic functions on Lipschitz domains", in Ryan, J. (ed.), Clifford Algebras in Analysis and Related Topics...

states the following: If U is an open subset of Rn and f: U → Rm is Lipschitz continuous, then f is differentiable almost everywhere in U; that is,...

= 1 {\displaystyle \alpha =1} is referred to as Lipschitz continuity. That is, a function is Lipschitz continuous if there is a constant K such that the...