scale convolution of two functions s ( t ) {\displaystyle s(t)} and r ( t ) {\displaystyle r(t)} , also known as their logarithmic convolution or log-volution...
2 KB (302 words) - 23:36, 15 September 2024
Index of logarithm articles (redirect from List of logarithmic topics)
distribution Logarithmic algorithm Logarithmic convolution Logarithmic decrement Logarithmic derivative Logarithmic differential Logarithmic differentiation...
3 KB (230 words) - 13:13, 22 February 2025
convolution Logarithmic convolution Vandermonde convolution Convolution, in digital image processing, with a Kernel (image processing) Convolutional code...
875 bytes (115 words) - 21:17, 12 October 2022
In convex analysis, a non-negative function f : Rn → R+ is logarithmically concave (or log-concave for short) if its domain is a convex set, and if it...
10 KB (1,319 words) - 19:51, 17 July 2025
obtain the convolution of a and b, according to the usual convolution theorem. Let us also be more precise about what type of convolution is required...
11 KB (1,570 words) - 16:02, 23 April 2025
Time complexity (redirect from Logarithmic time)
input cannot take logarithmic time, as the time taken for reading an input of size n is of the order of n. An example of logarithmic time is given by dictionary...
41 KB (4,997 words) - 07:38, 21 July 2025
density is a logarithmically concave function. Thus, any Gaussian measure is log-concave. The Prékopa–Leindler inequality shows that a convolution of log-concave...
2 KB (242 words) - 01:47, 15 January 2023
transforms, list of Fourier-related transforms Kernel (integral operator) Convolution Radon transform Buffon's needle Hadwiger's theorem mean width intrinsic...
2 KB (221 words) - 02:51, 2 May 2022
3SUM (section Convolution sum)
S2CID 30368541 Chan, Timothy M. (2020), "More logarithmic-factor speedups for 3SUM, (median,+)-convolution, and some geometric 3SUM-hard problems", ACM...
17 KB (2,676 words) - 07:02, 30 June 2025
before the first success (i.e. one less). The Hermite distribution The logarithmic (series) distribution The mixed Poisson distribution The negative binomial...
22 KB (2,620 words) - 07:59, 2 May 2025
Analog signal processing (section Convolution)
_{a}^{b}x(\tau )h(t-\tau )\,d\tau } That is the convolution integral and is used to find the convolution of a signal and a system; typically a = -∞ and...
10 KB (1,621 words) - 22:10, 20 July 2025
f(q)b ... While the Dirichlet convolution of two multiplicative functions is multiplicative, the Dirichlet convolution of two completely multiplicative...
6 KB (1,008 words) - 09:43, 9 August 2024
Arithmetic function (section Logarithmic derivative)
called the Dirichlet convolution of a and b, and is denoted by a ∗ b {\displaystyle a*b} . A particularly important case is convolution with the constant...
53 KB (7,555 words) - 01:12, 6 April 2025
Spectral leakage (section Convolution)
between s(t) and a Dirac comb function. The spectrum of a product is the convolution between S(f) and another function, which inevitably creates the new frequency...
25 KB (2,926 words) - 21:43, 23 May 2025
is the particle velocity, ∗ {\displaystyle *} is the convolution operator, z−1 is the convolution inverse of the specific acoustic impedance, hence the...
28 KB (3,053 words) - 13:23, 12 July 2025
intervals are 20 Hz wide. Note that spectra are often plotted with a logarithmic frequency axis rather than a linear one, in which case equal physical...
29 KB (3,597 words) - 17:25, 25 April 2025
Hence, y ( n ) = x ( n ) ∗ h ( n ) {\displaystyle y(n)=x(n)*h(n)} (convolution) As speech is not stationary signal, it is divided into overlapped frames...
16 KB (2,138 words) - 22:54, 25 July 2025
technical school in Paris. In 1791, Prony embarked on the task of producing logarithmic and trigonometric tables for the French Cadastre (geographic survey)...
16 KB (1,857 words) - 16:41, 12 April 2025
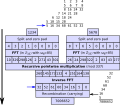
n + 1 {\displaystyle 2^{n}+1} ) can be calculated by evaluating the convolution of A , B {\displaystyle A,B} . Also, with g = 2 2 M ′ {\displaystyle...
26 KB (4,580 words) - 11:43, 4 June 2025
encountered when the usual arithmetic computations are performed on a logarithmic scale, as in log probability. Similar to multiplication operations in...
7 KB (1,152 words) - 12:49, 24 July 2025
interpolated at an arbitrary real argument x is obtained by the discrete convolution of those samples with the Lanczos kernel: S ( x ) = ∑ i = ⌊ x ⌋ − a +...
13 KB (1,496 words) - 03:11, 18 July 2025
] {\displaystyle \operatorname {E} \left[X^{-n}\right]} and the n-th logarithmic moment about zero is E [ ln n ( X ) ] . {\displaystyle \operatorname...
21 KB (3,068 words) - 20:19, 25 July 2025
{\displaystyle F} , the convolution of F {\displaystyle F} with itself, written F ∗ 2 {\displaystyle F^{*2}} and called the convolution square, is defined...
19 KB (2,725 words) - 05:28, 10 June 2025
f\star g} is the pdf of X + Y {\displaystyle X+Y} , we also have that the convolution of two log-concave functions is log-concave. Suppose that H(x,y) is a...
10 KB (1,160 words) - 03:09, 20 April 2025
integration kernels are then biperiodic functions; convolution by functions on the circle yields circular convolution. If one uses functions on the cyclic group...
13 KB (1,278 words) - 15:49, 29 July 2025
integral equations into algebraic polynomial equations, and by simplifying convolution into multiplication. For example, through the Laplace transform, the...
76 KB (9,703 words) - 21:25, 2 August 2025
figure. The product of two Gaussian functions is a Gaussian, and the convolution of two Gaussian functions is also a Gaussian, with variance being the...
30 KB (5,023 words) - 17:40, 4 April 2025
either linear or logarithmic, depending on what the graph is being used for. Audio would usually be represented with a logarithmic amplitude axis (probably...
20 KB (2,187 words) - 12:56, 6 July 2025
Iwaniec generalized the Elliott-Halberstam conjecture, using Dirichlet convolution of arithmetic functions related to the von Mangoldt function. The Elliott–Halberstam...
7 KB (995 words) - 10:49, 20 January 2025
polynomially in the number of qubits n {\displaystyle n} , which amounts to a logarithmic time complexity in the number of amplitudes and thereby the dimension...
75 KB (8,984 words) - 18:05, 29 July 2025