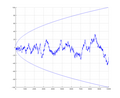
In number theory, the Mertens function is defined for all positive integers n as M ( n ) = ∑ k = 1 n μ ( k ) , {\displaystyle M(n)=\sum _{k=1}^{n}\mu (k)...

In mathematics, the Mertens conjecture is the statement that the Mertens function M ( n ) {\displaystyle M(n)} is bounded by ± n {\displaystyle \pm {\sqrt...

OEIS). In number theory another arithmetic function closely related to the Möbius function is the Mertens function, defined by M ( n ) = ∑ k = 1 n μ ( k )...

= Sophie Germain prime, centered square number, Mertens function zero 1014 = 210-10, Mertens function zero, sum of the nontriangular numbers between successive...

Franz Mertens (20 March 1840 – 5 March 1927) (also known as Franciszek Mertens) was a German-Polish mathematician. He was born in Schroda in the Grand...

super-prime 2093 – Mertens function zero 2095 – Mertens function zero 2096 – Mertens function zero 2097 – Mertens function zero 2099 – Mertens function zero, super-prime...

base 9, the Mertens function of 811 returns 0 812 = 22 × 7 × 29, admirable number, pronic number, balanced number, the Mertens function of 812 returns...

nine consecutive primes (29 + 31 + 37 + 41 + 43 + 47 + 53 + 59 + 61) Mertens function returns 0, Member of the Mian–Chowla sequence. 402 = 2 × 3 × 67, sphenic...

Schröder–Hipparchus number, Mertens function(903) returns 0, little Schroeder number 904 = 23 × 113 or 113 × 8, refactorable number, Mertens function(904) returns 0...

+ 211), Mertens function(607) = 0, balanced prime, strictly non-palindromic number, Mersenne prime exponent 608 = 25 × 19, Mertens function(608) = 0...

– Mertens function zero 8011 – Mertens function zero, super-prime 8012 – Mertens function zero 8017 – Mertens function zero 8021 – Mertens function zero...

61, Mertens function(793) = 0, star number, happy number 794 = 2 × 397 = 16 + 26 + 36, nontotient 795 = 3 × 5 × 53, sphenic number, Mertens function(795)...

centered hexagonal number, and Mertens function returns 0. 332 = 22 × 83, Mertens function returns 0. 333 = 32 × 37, Mertens function returns 0; repdigit; 2333...

consecutive primes (7 + 11 + 13 + 17 + 19 + 23 + 29 + 31). Given 150, the Mertens function returns 0. 150 is conjectured to be the only minimal difference greater...

(ed.). "Sequence A051402 (Inverse Mertens function: smallest k such that |M(k)| is n, where M(x) is Mertens's function A002321.)". The On-Line Encyclopedia...

362=2\times 181=\sigma _{2}(19)} : sum of squares of divisors of 19, Mertens function returns 0, nontotient, noncototient. 364 = 2 2 × 7 × 13 {\displaystyle...

hand, the first two integers that return 0 {\displaystyle 0} for the Mertens function (2 and 39) have a difference of 37, where their product (2 × 39) is...

Frank Mertens (born 1961), German keyboardist and composer Franz Mertens (1840–1927), German mathematician Mertens conjecture, Mertens function, Mertens' theorems...

Riemann hypothesis is equivalent to this bound for the Möbius function μ and the Mertens function M derived in the same way from it. In other words, the Riemann...

the sum of the digits in its prime factorization (13). Given 58, the Mertens function returns 0 {\displaystyle 0} , the fourth such number to do so. The...

it is also the fiftieth number to return 0 {\displaystyle 0} in the Mertens function. While the twenty-first prime number 73 is the largest member of Bhargava's...

^{-1}} -weighted summatory functions are related to the Mertens function, or weighted summatory functions of the Moebius function. In fact, we have that the...

as the sum of the cubes of the first three primes. Given 160, the Mertens function returns 0. 160 is the smallest number n with exactly 12 solutions to...

the sum of the first twenty positive even numbers. a zero of the Mertens function and is sparsely totient. a pronic number. The least common multiple...

analytic number theory, Mertens' theorems are three 1874 results related to the density of prime numbers proved by Franz Mertens. In the following, let...

prime. For the Mertens function, M ( 541 ) = 0. {\displaystyle M(541)=0.} 542 = 2 × 271. It is: a nontotient. the sum of totient function for the first...

the sum of the first three powers of 3 (31 + 32 + 33). Given 39, the Mertens function returns 0. 39 is the smallest natural number which has three partitions...

is an octagonal number. It is also a Cullen number. Given 65, the Mertens function returns 0. This number is the magic constant of a 5x5 normal magic...

palindromic in any base between base 2 and base 161. Given 163, the Mertens function returns 0, it is the fourth prime with this property, the first three...

thirty-second number to return 0 for the Mertens function M(n). Sloane, N. J. A. (ed.). "Sequence A002088 (Sum of totient function)". The On-Line Encyclopedia of...