multiple gamma function Γ N {\displaystyle \Gamma _{N}} is a generalization of the Euler gamma function and the Barnes G-function. The double gamma function...

mathematics, the gamma function (represented by Γ, capital Greek letter gamma) is the most common extension of the factorial function to complex numbers...

In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems...

reciprocal gamma function is the function f ( z ) = 1 Γ ( z ) , {\displaystyle f(z)={\frac {1}{\Gamma (z)}},} where Γ(z) denotes the gamma function. Since...

The gamma function is an important special function in mathematics. Its particular values can be expressed in closed form for integer, half-integer, and...

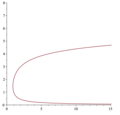
mathematics, the inverse gamma function Γ − 1 ( x ) {\displaystyle \Gamma ^{-1}(x)} is the inverse function of the gamma function. In other words, y = Γ...

In mathematics, a multivalued function, multiple-valued function, many-valued function, or multifunction, is a function that has two or more values in...

distribution functions of the gamma distribution vary based on the chosen parameterization, both offering insights into the behavior of gamma-distributed...

the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial...

Barnes G-function G ( z ) {\displaystyle G(z)} is a function that is an extension of superfactorials to the complex numbers. It is related to the gamma function...

that gamma globulin causes the spleen to ignore the antibody-tagged platelets, thus allowing them to survive and function. Another theory on how gamma globulin...

{\displaystyle q} -gamma function, or basic gamma function, is a generalization of the ordinary gamma function closely related to the double gamma function. It was...

Γ₀ or Gamma 0 may refer to: Feferman–Schütte ordinal Hecke congruence subgroup, Γ₀(n) the multiple gamma function, Γn, for n = 0, as used in an inductive...

distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution f ( x ; x 0 , γ ) {\displaystyle f(x;x_{0},\gamma )} is the distribution...

gamma function Laguerre polynomials Parabolic cylinder function (or Weber function) Poisson–Charlier function Toronto functions Whittaker functions Mκ...

{d} x} is the gamma function. The Riemann zeta function is defined for other complex values via analytic continuation of the function defined for σ >...

the multiple gamma function", Trans. Camb. Philos. Soc., 19: 374–425 Friedman, Eduardo; Ruijsenaars, Simon (2004), "Shintani–Barnes zeta and gamma functions"...

The theorem characterizes the gamma function, defined for x > 0 by Γ ( x ) = ∫ 0 ∞ t x − 1 e − t d t {\displaystyle \Gamma (x)=\int _{0}^{\infty }t^{x-1}e^{-t}\...

V(x;\sigma ,\gamma )={\frac {\operatorname {Re} [w(z)]}{{\sqrt {2\pi }}\,\sigma }},} where Re[w(z)] is the real part of the Faddeeva function evaluated for...

_{K})^{\beta }}={\tau _{K} \over \beta }\Gamma {\left({\frac {1}{\beta }}\right)}} where Γ is the gamma function. For exponential decay, ⟨τ⟩ = τK is recovered...

{\displaystyle \gamma _{2}={\frac {-6\Gamma _{1}^{4}+12\Gamma _{1}^{2}\Gamma _{2}-3\Gamma _{2}^{2}-4\Gamma _{1}\Gamma _{3}+\Gamma _{4}}{[\Gamma _{2}-\Gamma _{1}^{2}]^{2}}}}...

{\displaystyle \Gamma (z)} is the well known gamma function defined by Γ ( z ) = ∫ 0 ∞ t z − 1 e − z d z , ℜ ( z ) > 0 {\displaystyle \Gamma (z)=\int _{0}^{\infty...

we can optimize γ {\displaystyle \gamma } by finding the γ {\displaystyle \gamma } value for which the loss function has a minimum: γ m = arg ⁡ min γ ∑...

Helmut Wielandt states that the complex gamma function and its scalar multiples are the only holomorphic functions on the positive complex half-plane that...

z ) {\displaystyle \Gamma (z+1)=z\Gamma (z)} . The Hankel contour can be used to help derive an expression for the Gamma function, based on the fundamental...

(Vepstas 2008). Bose integral is result of multiplication between Gamma function and Zeta function. One can begin with equation for Bose integral, then use series...

A gamma wave or gamma rhythm is a pattern of neural oscillation in humans with a frequency between 30 and 100 Hz, the 40 Hz point being of particular...

integrals of Green's functions and sums of the same. For example, if L = ( ∂ x + γ ) ( ∂ x + α ) 2 {\displaystyle L=\left(\partial _{x}+\gamma \right)\left(\partial...

α + β + γ = 180 ∘ , {\displaystyle \alpha +\beta +\gamma =180^{\circ },} as long as the functions occurring in the formulae are well-defined (the latter...

the function γ ( z ) = ( a z + b ) / ( c z + d ) {\textstyle \gamma (z)=(az+b)/(cz+d)} . The identification of functions with matrices makes function composition...