In mathematics, the n! conjecture is the conjecture that the dimension of a certain bi-graded module of diagonal harmonics is n!. It was made by A. M...

The abc conjecture (also known as the Oesterlé–Masser conjecture) is a conjecture in number theory that arose out of a discussion of Joseph Oesterlé and...

Goldbach's conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even natural...

the n conjecture is a conjecture stated by Browkin & Brzeziński (1994) as a generalization of the abc conjecture to more than three integers. Given n ≥...

proof of the Macdonald positivity conjecture and the n! conjecture involved showing that the isospectral Hilbert scheme of n points in a plane was Cohen–Macaulay...

In number theory, Goldbach's weak conjecture, also known as the odd Goldbach conjecture, the ternary Goldbach problem, or the 3-primes problem, is the...

problems in mathematics The Collatz conjecture is one of the most famous unsolved problems in mathematics. The conjecture asks whether repeating two simple...

In mathematics, a conjecture is a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or...

mathematics, the Birch and Swinnerton-Dyer conjecture (often called the Birch–Swinnerton-Dyer conjecture) describes the set of rational solutions to...

Catalan's conjecture (or Mihăilescu's theorem) is a theorem in number theory that was conjectured by the mathematician Eugène Charles Catalan in 1844...

collections of polynomials. Rota's basis conjecture: for matroids of rank n {\displaystyle n} with n {\displaystyle n} disjoint bases B i {\displaystyle B_{i}}...

In mathematics, the Hodge conjecture is a major unsolved problem in algebraic geometry and complex geometry that relates the algebraic topology of a non-singular...

In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers a, b,...

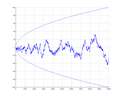
the Mertens conjecture is the statement that the Mertens function M ( n ) {\displaystyle M(n)} is bounded by ± n {\displaystyle \pm {\sqrt {n}}} . Although...

Ramanujan conjecture, due to Srinivasa Ramanujan (1916, p. 176), states that Ramanujan's tau function given by the Fourier coefficients τ(n) of the cusp...

conjecture or a slightly weaker version, they were able to show that there are infinitely many n such that at least two of n, n + 2, n + 6, n + 8, n +...

conjecture Kelvin's conjecture Kouchnirenko's conjecture Mertens conjecture Pólya conjecture, 1919 (1958) Ragsdale conjecture Schoenflies conjecture (disproved...

In number theory, the Pólya conjecture (or Pólya's conjecture) stated that "most" (i.e., 50% or more) of the natural numbers less than any given number...

conjecture quantifies asymptotically just how small they must be. It states that p n + 1 − p n = O ( ( log ⁡ p n ) 2 ) , {\displaystyle p_{n+1}-p_{n}=O((\log...

There are several conjectures known as the Hadwiger conjecture or Hadwiger's conjecture. They include: Hadwiger conjecture (graph theory), a relationship...

solution for every integer n ≥ 2 {\displaystyle n\geq 2} ? More unsolved problems in mathematics The Erdős–Straus conjecture is an unproven statement in...

conjecture is a disproved conjecture related to Fermat's Last Theorem. It was proposed by Leonhard Euler in 1769. It states that for all integers n and...

Jacobian conjecture is a famous unsolved problem concerning polynomials in several variables. It states that if a polynomial function from an n-dimensional...

In the mathematical field of geometric topology, the Poincaré conjecture (UK: /ˈpwæ̃kæreɪ/, US: /ˌpwæ̃kɑːˈreɪ/, French: [pwɛ̃kaʁe]) is a theorem about...

statement was known as the Taniyama–Shimura conjecture, Taniyama–Shimura–Weil conjecture, or the modularity conjecture for elliptic curves. The theorem states...

Legendre's conjecture, proposed by Adrien-Marie Legendre, states that there is a prime number between n 2 {\displaystyle n^{2}} and ( n + 1 ) 2 {\displaystyle...

Polignac's conjecture was made by Alphonse de Polignac in 1849 and states: For any positive even number n, there are infinitely many prime gaps of size n. In...

The Beal conjecture is the following conjecture in number theory: Unsolved problem in mathematics If A x + B y = C z {\displaystyle A^{x}+B^{y}=C^{z}}...

The conjecture states that for a polynomial f ( z ) = ( z − r 1 ) ⋯ ( z − r n ) , ( n ≥ 2 ) {\displaystyle f(z)=(z-r_{1})\cdots (z-r_{n}),\qquad (n\geq...

Erdős' conjecture on arithmetic progressions, often referred to as the Erdős–Turán conjecture, is a conjecture in arithmetic combinatorics (not to be...