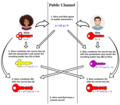
group theory, the Pohlig–Hellman algorithm, sometimes credited as the Silver–Pohlig–Hellman algorithm, is a special-purpose algorithm for computing discrete...

order of G should have a large prime factor to prevent use of the Pohlig–Hellman algorithm to obtain a or b. For this reason, a Sophie Germain prime q is...

his subsequent work in cryptography with Steve Pohlig (the Pohlig–Hellman algorithm) and others. Hellman addresses the National Security Agency’s (NSA)...

Diffie-Hellman key exchange, including the Pohlig–Hellman exponentiation cipher and the Pohlig–Hellman algorithm for computing discrete logarithms. That cipher...

Baby-step giant-step Index calculus algorithm Pohlig–Hellman algorithm Pollard's rho algorithm for logarithms Euclidean algorithm: computes the greatest common...

the Pohlig–Hellman algorithm has a smaller algorithmic complexity, and potentially solves the same problem. The baby-step giant-step algorithm is a generic...

the Diffie-Hellman cryptosystem which relies on the discrete logarithm. Merkle's Stanford University dissertation (1979) was credited by Pohlig (1977) and...

Index calculus algorithm Number field sieve Pohlig–Hellman algorithm Pollard's rho algorithm for logarithms Pollard's kangaroo algorithm (aka Pollard's...

{O}}({\sqrt {n}})} . If used together with the Pohlig–Hellman algorithm, the running time of the combined algorithm is O ( p ) {\displaystyle {\mathcal {O}}({\sqrt...

phenomena, then Shor's algorithm could be used to break public-key cryptography schemes, such as The RSA scheme The finite-field Diffie–Hellman key exchange The...

multiplication algorithm is an algorithm (or method) to multiply two numbers. Depending on the size of the numbers, different algorithms are more efficient...

The Tonelli–Shanks algorithm (referred to by Shanks as the RESSOL algorithm) is used in modular arithmetic to solve for r in a congruence of the form r2...

his subsequent work in cryptography with Steve Pohlig (the Pohlig–Hellman algorithm) and others. Hellman addresses the National Security Agency's (NSA)...

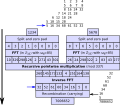
The Karatsuba algorithm is a fast multiplication algorithm for integers. It was discovered by Anatoly Karatsuba in 1960 and published in 1962. It is a...

chip used a data encryption algorithm called Skipjack to transmit information and the Diffie–Hellman key exchange-algorithm to distribute the public keys...

and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common...

theory, Williams's p + 1 algorithm is an integer factorization algorithm, one of the family of algebraic-group factorisation algorithms. It was invented by...

y {\displaystyle y} and k {\displaystyle k} be non-negative integers. Algorithms that compute (the decimal representation of) y {\displaystyle {\sqrt {y}}}...

composite return probably prime Using fast algorithms for modular exponentiation, the running time of this algorithm is O(k·log3 n), where k is the number...

The binary GCD algorithm, also known as Stein's algorithm or the binary Euclidean algorithm, is an algorithm that computes the greatest common divisor...

Pollard's rho algorithm is an algorithm for integer factorization. It was invented by John Pollard in 1975. It uses only a small amount of space, and...

The Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen...

efficient non-quantum integer factorization algorithm is known. However, it has not been proven that such an algorithm does not exist. The presumed difficulty...

Pollard's p − 1 algorithm is a number theoretic integer factorization algorithm, invented by John Pollard in 1974. It is a special-purpose algorithm, meaning...

In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking...

the field of public-key cryptography, where it is used in both Diffie–Hellman key exchange and RSA public/private keys. Modular exponentiation is the...

A primality test is an algorithm for determining whether an input number is prime. Among other fields of mathematics, it is used for cryptography. Unlike...

difficult, but in this case it can be done efficiently using the Pohlig–Hellman algorithm because M {\displaystyle M} is a smooth number. A test site is...

In computational number theory, Cipolla's algorithm is a technique for solving a congruence of the form x 2 ≡ n ( mod p ) , {\displaystyle x^{2}\equiv...

primality test and cyclotomic AKS test) is a deterministic primality-proving algorithm created and published by Manindra Agrawal, Neeraj Kayal, and Nitin Saxena...