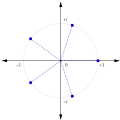
g is a primitive root modulo n if every number a coprime to n is congruent to a power of g modulo n. That is, g is a primitive root modulo n if for every...

modulo n, because they are zero divisors modulo n. A primitive root modulo n, is a generator of the group of units of the ring of integers modulo n....

In mathematics, a primitive root may mean: Primitive root modulo n in modular arithmetic Primitive nth root of unity amongst the solutions of zn = 1 in...

once). A generator of ( Z / n Z ) × {\displaystyle (\mathbb {Z} /n\mathbb {Z} )^{\times }} is called a primitive root modulo n. If there is any generator...

exponentiation Modulo (mathematics) Multiplicative group of integers modulo n Pisano period (Fibonacci sequences modulo n) Primitive root modulo n Quadratic...

In mathematics, the term primitive element can mean: Primitive root modulo n, in number theory Primitive element (field theory), an element that generates...

an element whose order equals the exponent, λ(n). Such an element is called a primitive λ-root modulo n. The Carmichael function is named after the American...

generators Character sum Multiplicative group of integers modulo n Primitive root modulo n Multiplicative character This is the standard definition; e...

of modular integers, see Root of unity modulo n. Every nth root of unity z is a primitive ath root of unity for some a ≤ n, which is the smallest positive...

multiplier a is an element of high multiplicative order modulo m (e.g., a primitive root modulo n), and the seed X0 is coprime to m. Other names are multiplicative...

\Phi _{n}} is irreducible if and only if p is a primitive root modulo n, that is, p does not divide n, and its multiplicative order modulo n is φ ( n ) {\displaystyle...

n is n − 1 for a prime n when a is a primitive root modulo n. If we can show a is primitive for n, we can show n is prime. Riesel (1994) pp.2-3 Barrus...

n) always divides φ(n). If the order of a is actually equal to φ(n), and therefore as large as possible, then a is called a primitive root modulo n....

φ(n) if and only if 10 is a primitive root modulo n. In particular, it follows that L(p) = p − 1 if and only if p is a prime and 10 is a primitive root...

function Noncototient Nontotient Euler's theorem Wilson's theorem Primitive root modulo n Multiplicative order Discrete logarithm Quadratic residue Euler's...

prime, then there exists a primitive root modulo n, or generator of the group (Z/nZ)*. Such a generator has order |(Z/nZ)*| = n−1 and both equivalences will...

Artin's conjecture on primitive roots states that a given integer a that is neither a square number nor −1 is a primitive root modulo infinitely many primes...

integers modulo n and Primitive root modulo n.   2 ω ( n ) ≤ d ( n ) ≤ 2 Ω ( n ) . {\displaystyle 2^{\omega (n)}\leq d(n)\leq 2^{\Omega (n)}.}     6...

quadratic residue modulo n if it is congruent to a perfect square modulo n; that is, if there exists an integer x such that x 2 ≡ q ( mod n ) . {\displaystyle...

includes work on Riemann zeta function, distribution of primes, and primitive root modulo n. In joint work with Dave Platt, he verified that the Riemann hypothesis...

n {\displaystyle n} th primitive root of unity if and only if n {\displaystyle n} is a divisor of q − 1 {\displaystyle q-1} ; if n {\displaystyle n}...

of degree m with coefficients in GF(p) = Z/pZ is a primitive polynomial if it is monic and has a root α in GF(pm) such that { 0 , 1 , α , α 2 , α 3 , …...

every primitive n-th root of unity is also a principal n {\displaystyle n} -th root of unity. In any ring, if n is a power of 2, then any n/2-th root of...

alternating sum of digits yields the value modulo ( b + 1 ) {\displaystyle (b+1)} . It helps to see the digital root of a positive integer as the position...

integer c is the hypotenuse of a primitive Pythagorean triple if and only if each prime factor of c is congruent to 1 modulo 4; that is, each prime factor...

0x80) /* GF modulo: if a has a nonzero term x^7, then must be reduced when it becomes x^8 */ a = (a << 1) ^ 0x11b; /* subtract (XOR) the primitive polynomial...

{\displaystyle b} modulo m {\displaystyle m} ") for b k ≡ a ( mod m ) {\displaystyle b^{k}\equiv a{\pmod {m}}} if b {\displaystyle b} is a primitive root of m {\displaystyle...

"divide by b" when working modulo a. Furthermore, if b1, b2 are both coprime with a, then so is their product b1b2 (i.e., modulo a it is a product of invertible...

protocol uses the multiplicative group of integers modulo p, where p is prime, and g is a primitive root modulo p. To guard against potential vulnerabilities...

perfect cubes must have digital root 1, 8 or 9. That is their values modulo 9 may be only 0, 1, and 8. Moreover, the digital root of any number's cube can be...