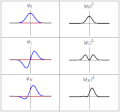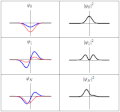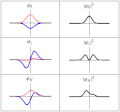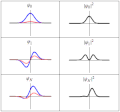
mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and...

applications, a Sturm–Liouville problem is a second-order linear ordinary differential equation of the form d d x [ p ( x ) d y d x ] + q ( x ) y = − λ w ( x...

for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs). In...

theory is a branch of the theory of ordinary differential equations relating to the class of solutions to periodic linear differential equations of the...

Stochastic differential equations can also be extended to differential manifolds. Stochastic differential equations originated in the theory of Brownian...

ordinary stochastic differential equations generalize ordinary differential equations. They have relevance to quantum field theory, statistical mechanics...

distinct subfields. Ordinary differential equations can be viewed as a subclass of partial differential equations, corresponding to functions of a single variable...

Eigenvalues and eigenvectors Hilbert–Schmidt theorem Spectral theory of ordinary differential equations Fixed point combinator Fourier transform eigenfunctions...

state, i.e. partial differential equations (PDEs) which are infinite dimensional, as opposed to ordinary differential equations (ODEs) having a finite...

In mathematics, in the field of ordinary differential equations, a nontrivial solution to an ordinary differential equation F ( x , y , y ′ ,   … ,   y...

helped to develop the Spectral theory of ordinary differential equations. He worked especially on second-order singular differential operators with a continuous...

separation of variables (also known as the Fourier method) is any of several methods for solving ordinary and partial differential equations, in which...

theory is a theory of integral equations. In the narrowest sense, Fredholm theory concerns itself with the solution of the Fredholm integral equation...

Control theory Oscillation theory Spectral theory of ordinary differential equations Submarine signals "Charles-François Sturm | Number Theory, Geometry...

from linear algebra and matrix theory. Spectral theory of ordinary differential equations part of spectral theory concerned with the spectrum and eigenfunction...

solution of partial differential equations. They are closely related to spectral methods, but complement the basis by an additional pseudo-spectral basis...

theory, they can be applied to other branches of mathematics. Fractional differential equations, also known as extraordinary differential equations,...

existence theorem (ordinary differential equations) Picard–Lindelöf theorem (ordinary differential equations) Shift theorem (differential operators) Sturm–Picone...

The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system.: 1–2  Its...

Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain differential equations. The...

following: a set of algebraic equations for steady-state problems; and a set of ordinary differential equations for transient problems. These equation sets are...

information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the...

Lyapunov exponent. Chaos theory began in the field of ergodic theory. Later studies, also on the topic of nonlinear differential equations, were carried out...

physics. In the theory of ordinary differential equations, spectral methods on a suitable Hilbert space are used to study the behavior of eigenvalues and...

geometries, graph theory, group theory, model theory, number theory, set theory, Ramsey theory, dynamical systems, and partial differential equations. Some problems...

The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having...

Fractional calculus Invariant differential operator Differential calculus over commutative algebras Lagrangian system Spectral theory Energy operator Momentum...

fact, considered parts of mathematical physics, while other closely related fields are. For example, ordinary differential equations and symplectic geometry...

of the same type, and often occur in fields such as calculus, differential equations and Riemannian geometry. In the theory of differential equations...

G\ast f} ). Through the superposition principle, given a linear ordinary differential equation (ODE), L y = f {\displaystyle Ly=f} , one can first solve L...