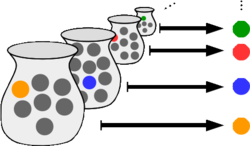
Tarski's undefinability theorem, stated and proved by Alfred Tarski in 1933, is an important limitative result in mathematical logic, the foundations...

theorems were among the first of several closely related theorems on the limitations of formal systems. They were followed by Tarski's undefinability...

Tarski's theorem may refer to the following theorems of Alfred Tarski: Tarski's theorem about choice Tarski's undefinability theorem Tarski's theorem...

theorem, Russell's paradox, Gödel's first incompleteness theorem, Turing's solution to the Entscheidungsproblem, and Tarski's undefinability theorem....

discoveries, most notably Tarski's undefinability theorem using the same formal technique Kurt Gödel used in his incompleteness theorems. Roughly, this states...

Deductive Sciences. Tarski's 1969 "Truth and proof" considered both Gödel's incompleteness theorems and Tarski's undefinability theorem, and mulled over...

arithmetic Tarski's undefinability theorem Church-Turing theorem of undecidability Löb's theorem Löwenheim–Skolem theorem Lindström's theorem Craig's theorem Cut-elimination...

Gödel's first incompleteness theorem Tarski's undefinability theorem Halting problem Kleene's recursion theorem Diagonalization (disambiguation) This disambiguation...

Łoś–Tarski preservation theorem Knaster–Tarski theorem (sometimes referred to as Tarski's fixed point theorem) Tarski's undefinability theorem Tarski–Seidenberg...

known as Tarski's undefinability theorem, was discovered independently by Gödel (when he was working on the proof of the incompleteness theorem) and by...

In mathematics, Tarski's theorem, proved by Alfred Tarski (1924), states that in ZF the theorem "For every infinite set A {\displaystyle A} , there is...

whether A(x) = 0 for some x are unsolvable. By contrast, the Tarski–Seidenberg theorem says that the first-order theory of the real field is decidable...

In set theory, Kőnig's theorem states that if the axiom of choice holds, I is a set, κ i {\displaystyle \kappa _{i}} and λ i {\displaystyle \lambda _{i}}...

Automated theorem proving (also known as ATP or automated deduction) is a subfield of automated reasoning and mathematical logic dealing with proving...

Schröder–Bernstein theorem. There is also a proof which uses Tarski's fixed point theorem. Myhill isomorphism theorem Netto's theorem, according to which...

In mathematical logic, the Löwenheim–Skolem theorem is a theorem on the existence and cardinality of models, named after Leopold Löwenheim and Thoralf...

Entscheidungsproblem Ordinal definable set Richard's paradox Tarski's undefinability theorem Turing, A. M. (1937), "On Computable Numbers, with an Application...

incompleteness theorem, because Tarski's theory lacks the expressive power needed to interpret Robinson arithmetic (Franzén 2005, pp. 25–26). Alfred Tarski worked...

Mathematical Platonism Primitive recursive functional Strange loop Tarski's undefinability theorem World Logic Day Gödel machine Kreisel, G. (1980). "Kurt Godel...

compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model. This theorem is an important...

defines F without reference to other sets. This is related to Tarski's undefinability theorem. The example of ZFC illustrates the importance of distinguishing...

and projective sets of reals; however for reasons related to Tarski's undefinability theorem the notion of a definable set of reals cannot be defined in...

excusable, it is not negligence. Gödel's incompleteness theorems: and Tarski's undefinability theorem Ignore all rules: To obey this rule, it is necessary...

Löwenheim–Skolem theorem gives elementary extensions of any infinite first-order structure of arbitrarily large cardinality. The Tarski–Vaught test (or Tarski–Vaught...

Education Thesis A Theory of Truth: The Liar Paradox and Tarski's Undefinability Theorem (1979) Philosophical work Era Contemporary philosophy Region...

In mathematical logic, Tarski's high school algebra problem was a question posed by Alfred Tarski. It asks whether there are identities involving addition...

Gödel's completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability...

theorem. In fact, Zermelo initially introduced the axiom of choice in order to formalize his proof of the well-ordering theorem. Set theory Tarski's theorem...

University of California, Berkeley—published his celebrated theorem on the undefinability of the notion of truth. Notable members of the Warsaw School of Mathematics...

is augmented with Tarski's axiom. Assuming that axiom turns the axioms of infinity, power set, and choice (7 – 9 above) into theorems. Many important statements...