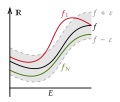
mathematical field of analysis, uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions ( f...

topological space. The convergence on Y X {\displaystyle Y^{X}} in the topology induced by the uniform extended norm is the uniform convergence, for sequences...

{\mathcal {G}}} (e.g. the "topology of uniform convergence on compact sets" or the "topology of compact convergence", see the footnote for more details)...

In mathematics, uniform absolute-convergence is a type of convergence for series of functions. Like absolute-convergence, it has the useful property that...

power series in complex analysis. Abel's uniform convergence test is a criterion for the uniform convergence of a series of functions dependent on parameters...

continuous as well. This theorem does not hold if uniform convergence is replaced by pointwise convergence. For example, let ƒn : [0, 1] → R be the sequence...

mathematics compact convergence (or uniform convergence on compact sets) is a type of convergence that generalizes the idea of uniform convergence. It is associated...

pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function. It is weaker than uniform convergence, to...

for convergence to occur. Determination of convergence requires the comprehension of pointwise convergence, uniform convergence, absolute convergence, Lp...

complete. Uniform convergence implies pointwise convergence and uniform Cauchy convergence. Uniform Cauchy convergence and pointwise convergence of a subsequence...

uniform convergence ≡ {\displaystyle \equiv } compact (uniform) convergence. Almost everywhere convergence Almost uniform convergence Lp convergence Convergence...

ƒn(x) = g(x − n). Then, ƒn converges pointwise to 0 but does not converge uniformly to 0. This criterion for uniform convergence is often useful in real...

Uniform convergence in probability is a form of convergence in probability in statistical asymptotic theory and probability theory. It means that, under...

is a test for determining whether an infinite series of functions converges uniformly and absolutely. It applies to series whose terms are bounded functions...

contrast, uniform convergence is a stronger type of convergence, in the sense that a uniformly convergent sequence of functions also converges pointwise...

there are various notions of the convergence of measures. For an intuitive general sense of what is meant by convergence of measures, consider a sequence...

with special regard to Augustin-Louis Cauchy and the concept of uniform convergence, in the light of non-standard analysis. Lakatos is concerned that...

continuous functions converges pointwise on a compact space and if the limit function is also continuous, then the convergence is uniform. If X {\displaystyle...

uniform space is uniformly continuous. Contraction mapping – Function reducing distance between all points Uniform convergence – Mode of convergence of...

Weierstrass' M-test, Abel's uniform convergence test, Dini's test, and the Cauchy criterion. More sophisticated types of convergence of a series of functions...

noted for introducing the Gudermannian function and the concept of uniform convergence, and for being the teacher of Karl Weierstrass, who was greatly influenced...

{\displaystyle X} equipped with the strong (dual) topology or the topology of uniform convergence on bounded subsets of X , {\displaystyle X,} where this topology...

M-test. The Cauchy convergence criterion states that a series ∑ n = 1 ∞ a n {\displaystyle \sum _{n=1}^{\infty }a_{n}} converges if and only if the sequence...

properties, such as completeness, uniform continuity and uniform convergence. Uniform spaces generalize metric spaces and topological groups, but the concept...

proof, recall that convergence in each limit involving f depends on the uniform continuity of f, which implies a rate of convergence dependent on f 's...

of mathematics, Egorov's theorem establishes a condition for the uniform convergence of a pointwise convergent sequence of measurable functions. It is...

notions of convergence of sequences of random variables, including convergence in probability, convergence in distribution, and almost sure convergence. The...

established uniform convergence on compact sets, the mean value property is not available in this more general setting, and so the proof of convergence to a...

gives a sufficient condition for the convergence of expected values of random variables. Lebesgue's dominated convergence theorem. Let ( f n ) {\displaystyle...

In mathematics normal convergence is a type of convergence for series of functions. Like absolute-convergence, it has the useful property that it is preserved...