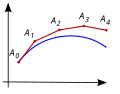
Runge–Kutta methods are methods for the numerical solution of the ordinary differential equation d y d t = f ( t , y ) . {\displaystyle {\frac {dy}{dt}}=f(t...

on the large class of Runge–Kutta methods. The novelty of Fehlberg's method is that it is an embedded method from the Runge–Kutta family, meaning that...

Runge–Kutta methods (English: /ˈrʊŋəˈkʊtɑː/ RUUNG-ə-KUUT-tah) are a family of implicit and explicit iterative methods, which include the Euler method...

basic explicit method for numerical integration of ordinary differential equations and is the simplest Runge–Kutta method. The Euler method is named after...

refer to Heun's method, for further clarity see List of Runge–Kutta methods. The name of the method comes from the fact that in the formula above, the...

differentiation methods (BDF), whereas implicit Runge–Kutta methods include diagonally implicit Runge–Kutta (DIRK), singly diagonally implicit Runge–Kutta (SDIRK)...

Wilhelm Kutta (German: [ˈkʊta]; 3 November 1867 – 25 December 1944) was a German mathematician. In 1901, he co-developed the Runge–Kutta method, used to...

gives the fourth-order solution. Adaptive Runge–Kutta methods List of Runge–Kutta methods Jeff R. Cash, Professor of Numerical Analysis, Imperial College London...

method or DOPRI method, is an embedded method for solving ordinary differential equations (ODE). The method is a member of the Runge–Kutta family of ODE...

Newell's car-following model Microscopic traffic flow model List of Runge–Kutta methods Traffic simulation traffic-simulation.de https://traffic-simulation...

includes parts of the imaginary axis, such as the fourth order Runge-Kutta method, is used. This makes the SAT technique an attractive method of imposing boundary...

Milstein method — a method with strong order one Runge–Kutta method (SDE) — generalization of the family of Runge–Kutta methods for SDEs Methods for solving...

analysis) Runge–Kutta method (numerical analysis) Sainte-Laguë method (voting systems) Schulze method (voting systems) Sequential Monte Carlo method Simplex...

second-order method in time. It is implicit in time, can be written as an implicit Runge–Kutta method, and it is numerically stable. The method was developed...

Single-step methods (such as Euler's method) refer to only one previous point and its derivative to determine the current value. Methods such as Runge–Kutta take...

standard techniques such as Euler's method or the Runge–Kutta method. In the second step above, a global system of equations is generated from the element...

g. order of Cholesky decomposition computations, maximum error in Chebyshev interpolation, and maximum stable step length using Runge-Kutta.) The Hans...

although those methods leverage heuristics that involve guessing and do not work for all inhomogeneous linear differential equations. Variation of parameters...

high-frequency content. Runge-Kutta method List of Runge–Kutta methods Numerical ordinary differential equations Linear multistep method Lie group integrator...

a1/a2 and a0/a2 are analytic functions. The power series method calls for the construction of a power series solution f = ∑ k = 0 ∞ A k z k . {\displaystyle...

numerical methods for the solution of ordinary differential equations. Butcher works on multistage methods for initial value problems, such as Runge-Kutta and...

in physics simulations a similar adaptive step method can be achieved using adaptive Runge-Kutta methods. The technique dates back to at least the 1980s;...

mathematician Runge–Kutta methods for numerical analysis Runge's phenomenon, a problem in the field of numerical analysis Runge's theorem Laplace–Runge–Lenz vector...

In mathematics, in the area of numerical analysis, Galerkin methods are a family of methods for converting a continuous operator problem, such as a differential...

solution which involves a nonelementary integral. This same method is used to solve the period of a simple pendulum. Integrating factors are useful for solving...

In mathematics, separation of variables (also known as the Fourier method) is any of several methods for solving ordinary and partial differential equations...

Initial condition Integral equations Numerical methods for ordinary differential equations Numerical methods for partial differential equations Picard–Lindelöf...

{dF(x)}{dx}}=f(x),\quad F(a)=0.} Numerical methods for ordinary differential equations, such as Runge–Kutta methods, can be applied to the restated problem...

and Wilhelm Kutta developed significant improvements to Euler's method around 1900. These gave rise to the large group of Runge-Kutta methods, which form...

x0*x1-(8/3)*x2]; n=100 h=0.1 tlist,y=Runge_Kutta(Lorenz,v,a,b,h,n) #Runge_Kutta(f,v,0,b,h,n) #print(tlist) #print(y) P1=list_plot([[tlist[i],y[i][0]] for i...