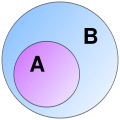
and logic, Ackermann set theory (AST, also known as A ∗ / V {\displaystyle A^{*}/V} ) is an axiomatic set theory proposed by Wilhelm Ackermann in 1956....

in December 1962. Ackermann's bijection Ackermann coding Ackermann function Ackermann ordinal Ackermann set theory Hilbert–Ackermann system Entscheidungsproblem...

set theory Morse–Kelley set theory Tarski–Grothendieck set theory Ackermann set theory Type theory New Foundations Positive set theory Internal set theory...

Wilhelm Ackermann Ackermann function Ackermann ordinal Ackermann set theory Ackermann steering geometry, in mechanical engineering Ackermann's formula...

Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Although objects of any...

where BIT denotes the BIT predicate. The Ackermann coding can be used to construct a model of finitary set theory in the natural numbers. More precisely...

In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in...

In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable...

"Set Theory", Stanford Encyclopedia of Philosophy, Metaphysics Research Lab, Stanford University Suppes, Patrick (1972) [1960], Axiomatic Set Theory,...

Zermelo–Fraenkel set theory; ZF, ZFC; Von Neumann–Bernays–Gödel set theory; NBG; (finitely axiomatizable) Ackermann set theory; Scott–Potter set theory New Foundations;...

In set theory, the union (denoted by ∪) of a collection of sets is the set of all elements in the collection. It is one of the fundamental operations...

In set theory, Kőnig's theorem states that if the axiom of choice holds, I is a set, κ i {\displaystyle \kappa _{i}} and λ i {\displaystyle \lambda _{i}}...

of k {\displaystyle k} -subsets of an n {\displaystyle n} -element set. In set theory, the notation [ A ] k {\displaystyle [A]^{k}} is also common, especially...

In set theory and its applications throughout mathematics, a class is a collection of sets (or sometimes other mathematical objects) that can be unambiguously...

Naive set theory is any of several theories of sets used in the discussion of the foundations of mathematics. Unlike axiomatic set theories, which are...

In set theory, the complement of a set A, often denoted by A c {\displaystyle A^{c}} (or A′), is the set of elements not in A. When all elements in the...

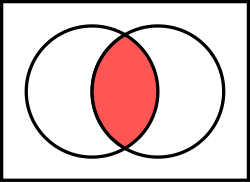
In set theory, the intersection of two sets A {\displaystyle A} and B , {\displaystyle B,} denoted by A ∩ B , {\displaystyle A\cap B,} is the set containing...

Axiomatic constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. The same first-order language...

are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous...

computability theory overlaps with proof theory and effective descriptive set theory. Basic questions addressed by computability theory include: What...

Non-well-founded set theories are variants of axiomatic set theory that allow sets to be elements of themselves and otherwise violate the rule of well-foundedness...

In set theory, several ways have been proposed to construct the natural numbers. These include the representation via von Neumann ordinals, commonly employed...

contradictions within modern axiomatic set theory. Set theory as conceived by Georg Cantor assumes the existence of infinite sets. As this assumption cannot be...

General set theory (GST) is George Boolos's (1998) name for a fragment of the axiomatic set theory Z. GST is sufficient for all mathematics not requiring...

In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by V, is the class of hereditary...

Neumann–Bernays–Gödel set theory (NBG) is an axiomatic set theory that is a conservative extension of Zermelo–Fraenkel–choice set theory (ZFC). NBG introduces...

In mathematics, and particularly in set theory, category theory, type theory, and the foundations of mathematics, a universe is a collection that contains...

Kripke–Platek set theory (KP), pronounced /ˈkrɪpki ˈplɑːtɛk/, is an axiomatic set theory developed by Saul Kripke and Richard Platek. The theory can be thought...

empty set or void set is the unique set having no elements; its size or cardinality (count of elements in a set) is zero. Some axiomatic set theories ensure...

enough fragment of arithmetic—including set theories such as Zermelo–Fraenkel set theory (ZF). These set theories cannot prove their own Gödel sentence—provided...