In complex analysis, a branch of mathematics, the antiderivative, or primitive, of a complex-valued function g is a function whose complex derivative...
7 KB (1,154 words) - 05:09, 31 March 2024
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function f is a differentiable...
21 KB (3,366 words) - 16:35, 30 April 2025
Holomorphic function (redirect from Complex differentiable)
holomorphic function on a Banach space over the field of complex numbers. Antiderivative (complex analysis) Antiholomorphic function Biholomorphy Cauchy's estimate...
25 KB (3,490 words) - 21:26, 15 June 2025
Morera's theorem (category Theorems in complex analysis)
having an antiderivative on D. The converse of the theorem is not true in general. A holomorphic function need not possess an antiderivative on its domain...
9 KB (1,404 words) - 20:23, 21 May 2025
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions...
18 KB (2,538 words) - 09:09, 12 May 2025
theorem (conformal mapping) Riemann–Roch theorem Amplitwist Antiderivative (complex analysis) Bôcher's theorem Cayley transform Harmonic conjugate Hilbert's...
5 KB (399 words) - 09:24, 23 July 2024
Contour integration (redirect from Integration using complex analysis)
mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane. Contour integration...
45 KB (9,666 words) - 06:50, 1 May 2025
Fundamental theorem of calculus (category Theorems in real analysis)
any antiderivative F between the ends of the interval. This greatly simplifies the calculation of a definite integral provided an antiderivative can be...
31 KB (4,883 words) - 12:15, 2 May 2025
by a complex number of modulus 1 acts as a rotation. The complex plane is sometimes called the Argand plane or Gauss plane. In complex analysis, the complex...
31 KB (4,502 words) - 23:12, 6 May 2025
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along...
15 KB (3,101 words) - 12:03, 13 December 2024
Zeros and poles (redirect from Zero (complex analysis))
In complex analysis (a branch of mathematics), a pole is a certain type of singularity of a complex-valued function of a complex variable. It is the simplest...
9 KB (1,479 words) - 11:37, 3 May 2025
Cauchy's integral formula (category Theorems in complex analysis)
formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk...
25 KB (4,364 words) - 04:10, 17 May 2025
In complex analysis, Liouville's theorem, named after Joseph Liouville (although the theorem was first proven by Cauchy in 1844), states that every bounded...
14 KB (2,330 words) - 21:13, 31 March 2025
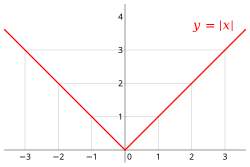
Absolute value (redirect from Modulus of complex number)
not a complex antiderivative because complex antiderivatives can only exist for complex-differentiable (holomorphic) functions, which the complex absolute...
27 KB (3,477 words) - 09:59, 20 April 2025
Line integral (redirect from Complex line integral)
complex analysis, the line integral is defined in terms of multiplication and addition of complex numbers. Suppose U is an open subset of the complex...
21 KB (3,183 words) - 03:16, 18 March 2025
Cauchy–Riemann equations (category Complex analysis)
In the field of complex analysis in mathematics, the Cauchy–Riemann equations, named after Augustin Cauchy and Bernhard Riemann, consist of a system of...
34 KB (5,011 words) - 14:50, 1 April 2025
Cauchy's integral theorem (category Theorems in complex analysis)
and end point b {\displaystyle b} . If F {\displaystyle F} is a complex antiderivative of f {\displaystyle f} , then ∫ γ f ( z ) d z = F ( b ) − F ( a...
10 KB (1,643 words) - 15:23, 27 May 2025
areas below are negative. Integrals also refer to the concept of an antiderivative, a function whose derivative is the given function; in this case, they...
69 KB (9,288 words) - 18:38, 23 May 2025
Residue theorem (category Theorems in complex analysis)
In complex analysis, the residue theorem, sometimes called Cauchy's residue theorem, is a powerful tool to evaluate line integrals of analytic functions...
13 KB (3,290 words) - 09:31, 29 January 2025
Integral of inverse functions (redirect from Antiderivative of inverse functions)
functions can be computed by means of a formula that expresses the antiderivatives of the inverse f − 1 {\displaystyle f^{-1}} of a continuous and invertible...
10 KB (1,696 words) - 03:08, 20 April 2025
Laurent series (category Complex analysis)
{\displaystyle f(z)} . Laurent series with complex coefficients are an important tool in complex analysis, especially to investigate the behavior of functions...
16 KB (2,675 words) - 20:24, 29 December 2024
it relates the values of antiderivatives to definite integrals. Because it is usually easier to compute an antiderivative than to apply the definition...
76 KB (8,805 words) - 00:02, 20 June 2025
Sine and cosine (redirect from Complex sine and cosine)
obtained by using the integral with a certain bounded interval. Their antiderivatives are: ∫ sin ( x ) d x = − cos ( x ) + C ∫ cos ( x ) d x = sin...
55 KB (7,064 words) - 00:33, 30 May 2025
integrals are often useful. This page lists some of the most common antiderivatives. A compilation of a list of integrals (Integraltafeln) and techniques...
29 KB (5,610 words) - 14:00, 17 April 2025
Winding number (category Complex analysis)
algebraic topology, and they play an important role in vector calculus, complex analysis, geometric topology, differential geometry, and physics (such as in...
16 KB (2,292 words) - 13:53, 6 May 2025
rule or change of variables, is a method for evaluating integrals and antiderivatives. It is the counterpart to the chain rule for differentiation, and can...
20 KB (3,328 words) - 18:12, 21 May 2025
Argument principle (category Theorems in complex analysis)
In complex analysis, the argument principle (or Cauchy's argument principle) is a theorem relating the difference between the number of zeros and poles...
9 KB (1,612 words) - 07:49, 26 May 2025
Schwarz lemma (category Theorems in complex analysis)
{\displaystyle g_{Y}} . The classical Schwarz lemma is a result in complex analysis typically viewed to be about holomorphic functions from the open unit...
9 KB (1,728 words) - 21:29, 22 June 2025
Picard theorem (category Theorems in complex analysis)
In complex analysis, Picard's great theorem and Picard's little theorem are related theorems about the range of an analytic function. They are named after...
12 KB (998 words) - 14:19, 11 March 2025
functions. In complex analysis, a function is called analytic in an open set "U" if it is (complex) differentiable at each point in "U" and its complex derivative...
16 KB (2,233 words) - 23:44, 25 May 2025