algebra, a Cartesian tensor uses an orthonormal basis to represent a tensor in a Euclidean space in the form of components. Converting a tensor's components...

of tensor theory. For expositions of tensor theory from different points of view, see: Tensor Tensor (intrinsic definition) Application of tensor theory...

(electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), and general relativity (stress–energy tensor, curvature tensor, ...). In...

mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multilinear...

has often been used for Cartesian products of graphs, but is now more commonly used for another construction known as the tensor product of graphs. The...

two vectors is sometimes called an elementary tensor or a decomposable tensor. The elementary tensors span V ⊗ W {\displaystyle V\otimes W} in the sense...

Cauchy stress tensor (symbol ⁠ σ {\displaystyle {\boldsymbol {\sigma }}} ⁠, named after Augustin-Louis Cauchy), also called true stress tensor or simply stress...

abelian category, is not Cartesian closed. So the category of modules over a ring is not Cartesian closed. However, the functor tensor product − ⊗ M {\displaystyle...

G. The Cartesian product of graphs is not a product in the sense of category theory. Instead, the categorical product is known as the tensor product...

In mathematics and physics, a tensor field is a function assigning a tensor to each point of a region of a mathematical space (typically a Euclidean space...

elasticity tensor is a fourth-rank tensor describing the stress-strain relation in a linear elastic material. Other names are elastic modulus tensor and stiffness...

theoretical physics, the spin tensor is a quantity used to describe the rotational motion of particles in spacetime. The spin tensor has application in general...

_{u}\beta _{v}+\gamma _{u}\gamma _{v}\right).} Cartesian tensor Euler angles Kay, D. C. (1988). Tensor Calculus. Schaum’s Outlines. McGraw Hill. pp. 18–19...

deformation tensors. In 1839, George Green introduced a deformation tensor known as the right Cauchy–Green deformation tensor or Green's deformation tensor (the...

that is, Cartesian tensors of rank 1; and permittivity ε is a Cartesian tensor of rank 2. Strain and stress are, in principle, also rank-2 tensors. But conventionally...

In physics, the gyration tensor is a tensor that describes the second moments of position of a collection of particles S m n   = d e f   1 N ∑ i = 1 N...

stress-energy tensor The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor field quantity...

electromagnetism, the electromagnetic tensor or electromagnetic field tensor (sometimes called the field strength tensor, Faraday tensor or Maxwell bivector) is a...

metric field on M consists of a metric tensor at each point p of M that varies smoothly with p. A metric tensor g is positive-definite if g(v, v) > 0 for...

In multilinear algebra, a tensor contraction is an operation on a tensor that arises from the canonical pairing of a vector space and its dual. In components...

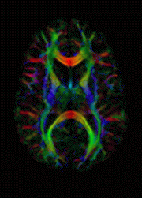
more gradient directions, sufficient to compute the diffusion tensor. The diffusion tensor model is a rather simple model of the diffusion process, assuming...

reflecting various orders of complexity. The quadrupole moment tensor Q is a rank-two tensor—3×3 matrix. There are several definitions, but it is normally...

notation and manipulation for tensors and tensor fields on a differentiable manifold, with or without a metric tensor or connection. It is also the modern...

In graph theory, the tensor product G × H of graphs G and H is a graph such that the vertex set of G × H is the Cartesian product V(G) × V(H); and vertices...

example, scalars, vectors, or tensors. Mathematical expressions involving these quantities in vector calculus and tensor analysis (such as the gradient...

graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which...

is also a spherical tensor operator. It is only for rank one that spherical tensor operators coincide with the Cartesian tensor operators. By developing...

a monoidal category where the monoidal ("tensor") product is the categorical product is called a cartesian monoidal category. Any category with finite...

unique point. The prototypical example of a coordinate system is the Cartesian coordinate system. In the plane, two perpendicular lines are chosen and...

a tensor of order n {\displaystyle n} and a tensor of order m {\displaystyle m} is a tensor of order n + m − 2 {\displaystyle n+m-2} , see Tensor contraction...