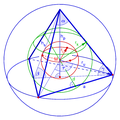
polyhedron with a circumscribed sphere, all faces have circumscribed circles, the circles where the plane of the face meets the circumscribed sphere. Descartes...
6 KB (743 words) - 12:45, 28 April 2025
definitions for the 'inspheres' of their polyhedra. Circumscribed sphere Inscribed circle Midsphere Sphere packing Coxeter, H.S.M. Regular Polytopes 3rd Edn...
3 KB (314 words) - 05:56, 20 May 2022
order. For each solid Euclid finds the ratio of the diameter of the circumscribed sphere to the edge length. In Proposition 18 he argues that there are no...
54 KB (5,634 words) - 03:59, 17 May 2025
Cube (section Relation to the spheres)
the sphere tangent to the edges of a cube, with radius 2 2 a {\textstyle {\frac {\sqrt {2}}{2}}a} . The circumscribed sphere of a cube is the sphere tangent...
62 KB (6,316 words) - 02:11, 22 May 2025
O(sn)} . Bounding volume Circumscribed sphere, circumscribed circle Larsson, Thomas (2008), "Fast and tight fitting bounding spheres", SIGRAD 2008: The Annual...
12 KB (1,515 words) - 14:14, 6 January 2025
term may refer to its circumradius, the radius of its circumscribed circle or circumscribed sphere. In either case, the radius may be more than half the...
10 KB (1,199 words) - 07:19, 18 May 2025
circumcircles of all triangles have empty interiors. By considering circumscribed spheres, the notion of Delaunay triangulation extends to three and higher...
29 KB (3,255 words) - 19:16, 18 March 2025
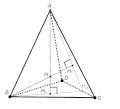
Tetrahedron (redirect from Twelve-point sphere)
For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere (the insphere) tangent to the tetrahedron's...
76 KB (9,506 words) - 04:09, 11 March 2025
the property that it is the symmetric point of the center of the circumscribed sphere with respect to the centroid. Hence the orthocenter coincides with...
4 KB (498 words) - 04:17, 21 October 2024
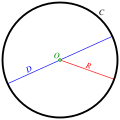
Circumcircle (redirect from Triangle Circumscribing)
In geometry, the circumscribed circle or circumcircle of a triangle is a circle that passes through all three vertices. The center of this circle is called...
27 KB (4,773 words) - 22:10, 29 April 2025
volume between the sphere and the circumscribed cylinder of that sphere (having the height and diameter equal to the diameter of the sphere). This may be proved...
41 KB (5,342 words) - 15:01, 12 May 2025
surface and extending this line on one side so that it intersects the circumscribed sphere at C; then B divides AC according to the golden section. This construction...
6 KB (727 words) - 20:27, 13 March 2023
order. For each solid, Euclid finds the ratio of the diameter of the circumscribed sphere to the edge length. In Proposition 18 he argues that there are no...
37 KB (3,764 words) - 16:24, 18 May 2025
Measuring angles directly to the surface of the ellipsoid, not to the circumscribed sphere, [ x y z ] = R [ cos γ cos λ cos γ sin λ sin γ ] {\displaystyle...
37 KB (5,912 words) - 21:24, 28 April 2025
Midsphere (category Spheres)
the radius of the inscribed sphere, 1 2 {\textstyle {\frac {1}{2}}} , and smaller than the radius of the circumscribed sphere, 3 2 {\textstyle {\frac {\sqrt...
25 KB (2,932 words) - 17:02, 24 January 2025
circumscribed parallelepiped is right-angled. We also have that a tetrahedron is a disphenoid if and only if the center in the circumscribed sphere and...
13 KB (1,532 words) - 09:02, 17 March 2025
Platonic solids and solved the problem of finding the ratio of the circumscribed sphere's diameter to the edge length. Following their identification with...
46 KB (4,617 words) - 02:17, 19 May 2025
a sphere centered on this point, as in the Dorman Luke construction (mentioned below). Failing that, for a polyhedron with a circumscribed sphere, inscribed...
18 KB (2,272 words) - 22:22, 14 March 2025
On the Sphere and Cylinder (Greek: Περὶ σφαίρας καὶ κυλίνδρου) is a treatise that was published by Archimedes in two volumes c. 225 BCE. It most notably...
6 KB (733 words) - 16:08, 16 April 2025
radius of a circumscribed sphere r u {\displaystyle r_{u}} (one that touches the octahedron at all vertices), the radius of an inscribed sphere r i {\displaystyle...
37 KB (3,708 words) - 18:19, 13 May 2025
midpoint between its Monge point and circumcenter (center of the circumscribed sphere). These three points define the Euler line of the tetrahedron that...
26 KB (4,242 words) - 05:08, 1 March 2025
same thing as "figure G is circumscribed about figure F". A circle or ellipse inscribed in a convex polygon (or a sphere or ellipsoid inscribed in a...
5 KB (650 words) - 19:50, 30 November 2023
Cylinder (section On the Sphere and Cylinder)
a sphere by exploiting the relationship between a sphere and its circumscribed right circular cylinder of the same height and diameter. The sphere has...
21 KB (2,928 words) - 12:00, 16 March 2025
Ideal polyhedron (category Spheres)
be represented in Euclidean geometry with all its vertices on a circumscribed sphere. Using linear programming, it is possible to test whether a polyhedron...
27 KB (3,229 words) - 08:46, 9 January 2025
polyhedron and projecting the resulting points and lines onto the circumscribed sphere. In the case of the tetrahedron, there are four faces and each face...
16 KB (1,771 words) - 04:06, 8 February 2024
looks like one from outside. A Kepler–Poinsot polyhedron covers its circumscribed sphere more than once, with the centers of faces acting as winding points...
32 KB (2,320 words) - 21:42, 21 May 2025
its own nature and special aim. There is therefore, as it were a circumscribed sphere in which each exercises its functions jure proprio". And in the Encyclical...
32 KB (4,713 words) - 16:02, 10 January 2025
one vertex, 3 edges, and 2 faces. This contraction distorts the circumscribed sphere original vertices. With all equilateral triangle faces, it has 2...
3 KB (270 words) - 05:26, 6 May 2025
Circumference (redirect from Circumference of a sphere)
less than 31/7 by calculating the perimeters of an inscribed and a circumscribed regular polygon of 96 sides. This method for approximating π was used...
9 KB (1,068 words) - 20:47, 11 May 2025
right angles. The midpoint of the longest edge is the center of the circumscribed sphere. The case when | v 0 v 1 | = | v 1 v 2 | = ⋯ = | v d − 1 v d | {\displaystyle...
10 KB (1,057 words) - 01:56, 22 May 2025