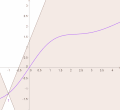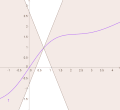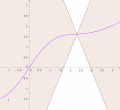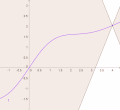
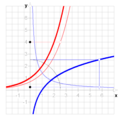
continuous function; there exist functions that are differentiable but not continuously differentiable (an example is given in the section Differentiability classes)...

function is differentiable just once on an open set, it is both infinitely differentiable and analytic on that set.[citation needed] Smooth functions...

that the value of the right sub-function is used in this position. For a piecewise-defined function to be differentiable on a given interval in its domain...

mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each...

Weierstrass function, named after its discoverer, Karl Weierstrass, is an example of a real-valued function that is continuous everywhere but differentiable nowhere...

and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally...

versions of the inverse function theorem for holomorphic functions, for differentiable maps between manifolds, for differentiable functions between Banach spaces...

mathematics, smooth functions (also called infinitely differentiable functions) and analytic functions are two very important types of functions. One can easily...

Allendoerfer, Carl B. (1974). "Theorems about Differentiable Functions". Calculus of Several Variables and Differentiable Manifolds. New York: Macmillan. pp. 54–88...

mechanical and electrical engineering. As a differentiable function of a complex variable is equal to the sum function given by its Taylor series (that is, it...

that interval. If a function is differentiable and convex then it is also continuously differentiable. A differentiable function of one variable is convex...

derivatives are the result of differentiating a function repeatedly. Given that f {\displaystyle f} is a differentiable function, the derivative of f {\displaystyle...

another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold...

to 1. Lipschitz continuous functions that are everywhere differentiable but not continuously differentiable The function f ( x ) = { x 2 sin ⁡ ( 1 /...

zero (note that this indicator function is not left differentiable at zero). If a real-valued, differentiable function f, defined on an interval I of...

an implicit function that is differentiable in some small enough neighbourhood of (a, b); in other words, there is a differentiable function f that is defined...

theorem or Rolle's lemma essentially states that any real-valued differentiable function that attains equal values at two distinct points must have at least...

properties: V is differentiable everywhere The derivative V ′ is bounded everywhere The derivative is not Riemann-integrable. The function is defined by...

C_{c}^{1}(\Omega ,\mathbb {R} ^{n})} is the set of continuously differentiable vector functions of compact support contained in Ω {\displaystyle \Omega } ...

The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change...

Jacobian matrix is not maximal. It extends further to differentiable maps between differentiable manifolds, as the points where the rank of the Jacobian...

function that is Fréchet differentiable at a point is necessarily continuous there and sums and scalar multiples of Fréchet differentiable functions are...

by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a typical differentiable function on a manifold...

of a scalar-valued differentiable function f {\displaystyle f} of several variables is the vector field (or vector-valued function) ∇ f {\displaystyle...

{d^{k}}{dx^{k}}}g(x).} Differentiable function – Mathematical function whose derivative exists Differential of a function – Notion in calculus Differentiation of integrals –...

calculus, the inverse function rule is a formula that expresses the derivative of the inverse of a bijective and differentiable function f in terms of the...

Taylor's theorem gives an approximation of a k {\textstyle k} -times differentiable function around a given point by a polynomial of degree k {\textstyle k}...

the Fabius function is an example of an infinitely differentiable function that is nowhere analytic, found by Jaap Fabius (1966). This function satisfies...

the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R , {\displaystyle f\colon U\to \mathbb...

can also be extended to differentiable manifolds. If f : M → R {\displaystyle f:M\to \mathbb {R} } is a differentiable function on a manifold M {\displaystyle...