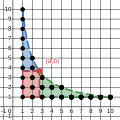
In number theory, the divisor summatory function is a function that is a sum over the divisor function. It frequently occurs in the study of the asymptotic...

related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function. The sum of positive divisors function σz(n)...

summation function for large x. A classical example of this phenomenon is given by the divisor summatory function, the summation function of d(n), the...

In mathematics, the greatest common divisor (GCD), also known as greatest common factor (GCF), of two or more integers, which are not all zero, is the...

\alpha ^{-1}} -weighted summatory functions are related to the Mertens function, or weighted summatory functions of the Moebius function. In fact, we have that...

called Euler's phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal...

constant. Given an additive function f {\displaystyle f} , let its summatory function be defined by M f ( x ) := ∑ n ≤ x f ( n ) {\textstyle {\mathcal {M}}_{f}(x):=\sum...

constants. The function ω ( n ) {\displaystyle \omega (n)} is related to divisor sums over the Möbius function and the divisor function, including: ∑ d...

divisor problem of computing asymptotic estimates for the summatory function of the divisor function. From we have ∑ d = 1 n M ( ⌊ n / d ⌋ ) = 1   . {\displaystyle...

algorithm. Sums involving the Möbius and von Mangolt function. Estimate of the divisor summatory function of the Dirichlet hyperbola method. In some formulations...

(f)=q^{2n}(1-q^{-1}).} Divisor summatory function Normal order of an arithmetic function Extremal orders of an arithmetic function Divisor sum identities Hardy...

mathematics, Dirichlet convolution (or divisor convolution) is a binary operation defined for arithmetic functions; it is important in number theory. It...

number-theoric functions include the divisor-counting function, the divisor summatory function and its modifications, and Euler's totient function. A prime...

average order summatory functions over an arithmetic function f ( n ) {\displaystyle f(n)} defined as a divisor sum of another arithmetic function g ( n ) {\displaystyle...

/ ln 2: 83  It is conjectured that the Mertens function, or summatory function of the Möbius function, satisfies lim sup n → ∞ | M ( x ) | x = + ∞ , {\displaystyle...

MR 1209991.. Luca, Florian; Marques, Diego (2010). "Perfect powers in the summatory function of the power tower". Journal de Théorie des Nombres de Bordeaux. 22...

{\displaystyle \mu (n)} is the Moebius function. Another unique Dirichlet series identity generates the summatory function of some arithmetic f evaluated at...

making fifty-eight the sixth noncototient; however, the totient summatory function over the first thirteen integers is 58. On the other hand, the Euler...

{\displaystyle |F_{n}|=1+\sum _{m=1}^{n}\varphi (m)=1+\Phi (n),} where Φ(n) is the summatory totient. We also have : | F n | = 1 2 ( 3 + ∑ d = 1 n μ ( d ) ⌊ n d ⌋...

\prod _{p}\left(1-{\frac {1}{p^{2}(p+1)}}\right)=0.881513...} The totient summatory constant OEIS: A065483: ∏ p ( 1 + 1 p 2 ( p − 1 ) ) = 1.339784... {\displaystyle...

{\displaystyle p^{5}} where p {\displaystyle p} is prime. 32 is the totient summatory function Φ ( n ) {\displaystyle \Phi (n)} over the first 10 integers, and the...

This yields the formula Let σ0(n) be the divisor-counting function, and let D(n) be its summatory function: D ( n ) = ∑ k = 1 n σ 0 ( k ) . {\displaystyle...

remainder terms of the summatory functions of both the sum-of-divisors function σ {\displaystyle \sigma } and the Euler function ϕ {\displaystyle \phi...

primes. 24, all Dirichlet characters mod n are real if and only if n is a divisor of 24. 25, the first centered square number besides 1 that is also a square...