the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial can be...
19 KB (2,911 words) - 11:02, 4 April 2025
in terms of elementary symmetric polynomials. This implies that every symmetric polynomial expression in the roots of a monic polynomial can alternatively...
21 KB (3,833 words) - 19:46, 29 March 2025
algebraic combinatorics, the ring of symmetric functions is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
27 KB (3,850 words) - 18:08, 27 February 2024
elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of polynomial irreducible...
20 KB (3,773 words) - 12:22, 22 April 2025
polynomial expression in complete homogeneous symmetric polynomials. The complete homogeneous symmetric polynomial of degree k in n variables X1, ..., Xn, written...
15 KB (3,192 words) - 19:43, 28 January 2025
Newton's identities (redirect from Newton's theorem on symmetric polynomials)
types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monic polynomial P in one...
35 KB (7,650 words) - 23:11, 16 April 2025
Symmetry in mathematics (section Symmetric polynomials)
fundamental symmetric polynomials. A theorem states that any symmetric polynomial can be expressed in terms of elementary symmetric polynomials, which implies...
21 KB (2,837 words) - 17:16, 5 January 2025
Aside from polynomial functions, tensors that act as functions of several vectors can be symmetric, and in fact the space of symmetric k {\displaystyle...
5 KB (873 words) - 01:02, 18 December 2023
Newton's inequalities (redirect from Elementary symmetric mean)
{\displaystyle e_{k}} denote the kth elementary symmetric polynomial in a1, a2, ..., an. Then the elementary symmetric means, given by S k = e k ( n k )...
2 KB (252 words) - 21:14, 14 April 2025
power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational...
6 KB (1,180 words) - 17:03, 10 April 2025
the i th elementary symmetric polynomial. The symmetric group Sn acts on the Xi by permuting them, and this induces an action on the polynomials in the...
9 KB (1,317 words) - 21:24, 21 February 2025
Chern class (section Chern polynomial)
σk are elementary symmetric polynomials. In other words, thinking of ai as formal variables, ck "are" σk. A basic fact on symmetric polynomials is that...
42 KB (7,508 words) - 13:07, 21 April 2025
a_{2},\ldots ,a_{k-j+1}).} The elementary symmetric polynomial e n {\displaystyle e_{n}} and the power sum symmetric polynomial p n {\displaystyle p_{n}} can...
32 KB (7,647 words) - 15:09, 27 June 2025
{1}{n^{2}}}={\frac {\pi ^{2}}{6}}.} Using formulae obtained from elementary symmetric polynomials, this same approach can be used to enumerate formulae for the...
44 KB (8,669 words) - 22:13, 22 June 2025
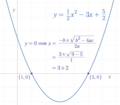
Quadratic formula (category Elementary algebra)
symmetric polynomials in α {\displaystyle \alpha } and β {\displaystyle \beta } . Specifically, they are the elementary symmetric polynomials –...
35 KB (5,787 words) - 19:29, 24 May 2025
Vieta's formulas (category Polynomials)
Gauss–Lucas theorem Properties of polynomial roots Rational root theorem Symmetric polynomial and elementary symmetric polynomial Ypma, Tjalling J. (1995). "Historical...
12 KB (2,587 words) - 10:40, 9 June 2025
Pieri's formula (category Symmetric functions)
the ring of symmetric functions, one obtains the dual Pieri rule for multiplying an elementary symmetric polynomial with a Schur polynomial: s μ e r =...
2 KB (242 words) - 08:56, 28 January 2024
Resultant (redirect from Polynomial resultant)
degree as elementary symmetric polynomial), then it is quasi-homogeneous of total weight de. If P and Q are homogeneous multivariate polynomials of respective...
46 KB (8,061 words) - 20:15, 4 June 2025
(Such a polynomial exists, because the expression is symmetric in the Xi and the elementary symmetric polynomials generate all symmetric polynomials.) Now...
12 KB (1,686 words) - 13:34, 28 May 2025
, … {\displaystyle k=0,1,2,3,\ldots } ) be the kth-degree elementary symmetric polynomial in the variables x i = tan θ i {\displaystyle x_{i}=\tan...
83 KB (12,419 words) - 02:33, 25 June 2025
That is, it satisfies the condition A skew-symmetric ⟺ A T = − A . {\displaystyle A{\text{ skew-symmetric}}\quad \iff \quad A^{\textsf {T}}=-A.} In terms...
19 KB (3,632 words) - 21:44, 14 June 2025
R_{F}} and its integral can be expressed as functions of the elementary symmetric polynomials in Δ x {\displaystyle \Delta x} , Δ y {\displaystyle \Delta...
14 KB (3,790 words) - 01:01, 11 May 2024
Galois theory (redirect from Galois group of a polynomial)
originated in the study of symmetric functions – the coefficients of a monic polynomial are (up to sign) the elementary symmetric polynomials in the roots. For...
33 KB (4,221 words) - 15:58, 21 June 2025
relation over Q {\displaystyle \mathbb {Q} } by using the fact that a symmetric polynomial whose arguments are all conjugates of one another gives a rational...
28 KB (4,778 words) - 00:16, 18 April 2025
For the remainder of this article, "symmetric group" will mean a symmetric group on a finite set. The symmetric group is important to diverse areas of...
46 KB (6,212 words) - 00:39, 20 June 2025
This issue doesn't arise when A is real and symmetric, resulting in a simple algorithm: % Given a real symmetric 3x3 matrix A, compute the eigenvalues % Note...
40 KB (4,870 words) - 04:25, 26 May 2025
Fundamental theorem of algebra (category Theorems about polynomials)
are symmetric polynomials in the zi with real coefficients. Therefore, they can be expressed as polynomials with real coefficients in the elementary symmetric...
51 KB (7,637 words) - 03:42, 7 June 2025
Maclaurin's inequality (category Symmetric functions)
{n \choose k}}}.} The numerator of this fraction is the elementary symmetric polynomial of degree k {\displaystyle k} in the n {\displaystyle n} variables...
2 KB (501 words) - 21:13, 14 April 2025
are simpler in the case of monic polynomials: The ith elementary symmetric function of the roots of a monic polynomial of degree n equals ( − 1 ) i c n...
7 KB (1,159 words) - 12:21, 13 October 2023
Discriminant (redirect from Discriminant of a polynomial)
every polynomial which is homogeneous and symmetric in the roots may be expressed as a quasi-homogeneous polynomial in the elementary symmetric functions...
41 KB (6,704 words) - 20:17, 23 June 2025