classical statistical mechanics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the tendency of the quantity H (defined below) to decrease in...

field of group theory, Lagrange's theorem states that if H is a subgroup of any finite group G, then | H | {\displaystyle |H|} is a divisor of | G | {\displaystyle...

In mathematics, the mean value theorem (or Lagrange's mean value theorem) states, roughly, that for a given planar arc between two endpoints, there is...

In complex analysis, Picard's great theorem and Picard's little theorem are related theorems about the range of an analytic function. They are named after...

The fundamental theorem of calculus is a theorem that links the concept of differentiating a function (calculating its slopes, or rate of change at every...

|\psi (X,t)|^{2}} may be accounted for by an H-theorem constructed in analogy to the Boltzmann H-theorem of statistical mechanics. Valentini's derivation...

N\hookrightarrow W} are homotopy equivalences. The h-cobordism theorem gives sufficient conditions for an h-cobordism to be trivial, i.e., to be C-isomorphic...

Schröder–Bernstein theorem states that, if there exist injective functions f : A → B and g : B → A between the sets A and B, then there exists a bijective function h :...

If h denotes the altitude in a right triangle and p and q the segments on the hypotenuse then the theorem can be stated as: h = p q {\displaystyle h={\sqrt...

|\psi (x,y,z,t)|^{2}} may be accounted for by a H-theorem constructed in analogy to the Boltzmann H-theorem of statistical mechanics. Valentini showed that...

In linear algebra and functional analysis, a spectral theorem is a result about when a linear operator or matrix can be diagonalized (that is, represented...

In mathematics and physics, the Poincaré recurrence theorem states that certain dynamical systems will, after a sufficiently long but finite time, return...

1982 by William Wootters and Wojciech H. Zurek as well as Dennis Dieks the same year). The aforementioned theorems do not preclude the state of one system...

that emerged in the first half of the 20th century. The theorem was first proved by Marshall H. Stone. Stone was led to it by his study of the spectral...

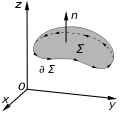
theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls, or simply the curl theorem,...

In calculus, Rolle's theorem or Rolle's lemma essentially states that any real-valued differentiable function that attains equal values at two distinct...

In calculus, the squeeze theorem (also known as the sandwich theorem, among other names) is a theorem regarding the limit of a function that is bounded...

Rouché's theorem, named after Eugène Rouché, states that for any two complex-valued functions f and g holomorphic inside some region K {\displaystyle...

specifically abstract algebra, the isomorphism theorems (also known as Noether's isomorphism theorems) are theorems that describe the relationship among quotients...

The Nyquist–Shannon sampling theorem is an essential principle for digital signal processing linking the frequency range of a signal and the sample rate...

fundamental theorem is a theorem which is considered to be central and conceptually important for some topic. For example, the fundamental theorem of calculus...

increasing according to the second law of thermodynamics, Boltzmann’s H-theorem used equations, which assumed a system (for example, a gas) was isolated...

version of Pappus's theorem shown in the second diagram. If the Pappus line u {\displaystyle u} and the lines g , h {\displaystyle g,h} have a point in common...

Gibbs elasticity Gibbs ensemble Gibbs entropy Gibbs free energy Gibbs H-theorem Gibbs' inequality Gibbs isotherm Gibbs lemma Gibbs measure Gibbs random...

In mathematics, the inverse function theorem is a theorem that asserts that, if a real function f has a continuous derivative near a point where its derivative...

product of 1-particle distributions. This in turn leads to Boltzmann's H-theorem of 1872, which attempted to use kinetic theory to show that the entropy...

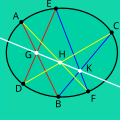
In projective geometry, Pascal's theorem (also known as the hexagrammum mysticum theorem, Latin for mystical hexagram) states that if six arbitrary points...

In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...

stated in terms of direct-current resistive circuits only, Thévenin's theorem states that "Any linear electrical network containing only voltage sources...

In multivariable calculus, the implicit function theorem is a tool that allows relations to be converted to functions of several real variables. It does...