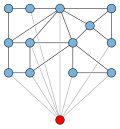
graph as a minor? More unsolved problems in mathematics In graph theory, the Hadwiger conjecture states that if G {\displaystyle G} is loopless and has no...

There are several conjectures known as the Hadwiger conjecture or Hadwiger's conjecture. They include: Hadwiger conjecture (graph theory), a relationship...

Total coloring conjecture, also called Behzad's conjecture (unsolved) List coloring conjecture (unsolved) Hadwiger conjecture (graph theory) (unsolved) Constraint...

In graph theory, the Hadwiger number of an undirected graph G is the size of the largest complete graph that can be obtained by contracting edges of G...

tree The Hadwiger conjecture relating coloring to clique minors The Hadwiger–Nelson problem on the chromatic number of unit distance graphs Jaeger's Petersen-coloring...

in Turán's theorem. Hadwiger's conjecture, still unproven, relates the size of the largest clique minor in a graph (its Hadwiger number) to its chromatic...

Appendix:Glossary of graph theory in Wiktionary, the free dictionary. This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes...

vertex. Hadwiger's name is also associated with several important unsolved problems in mathematics: The Hadwiger conjecture in graph theory, posed by...

important and difficult problems in graph theory (such as the cycle double cover conjecture and the 5-flow conjecture), one encounters an interesting but...

chromatic number of graphs include the Hadwiger conjecture stating that every graph with chromatic number k has a complete graph on k vertices as a minor...

H-minor-free graphs have treewidth O ( n ) {\displaystyle \scriptstyle O({\sqrt {n}})} . The Hadwiger conjecture in graph theory proposes that if a graph G does...

certain type of graph (called a snark in modern terminology) must be non-planar. In 1943, Hugo Hadwiger formulated the Hadwiger conjecture, a far-reaching...

In graph theory, a critical graph is an undirected graph all of whose proper subgraphs have smaller chromatic number. In such a graph, every vertex or...

Geometric graph theory in the broader sense is a large and amorphous subfield of graph theory, concerned with graphs defined by geometric means. In a stricter...

packings Kepler conjecture Quasicrystals Aperiodic tilings Periodic graph Finite subdivision rules Structural rigidity is a combinatorial theory for predicting...

Paul Seymour, and Robin Thomas (1993) of the Hadwiger conjecture for K6-minor-free graphs. If a graph has crossing number k {\displaystyle k} , it has...

as minors in a graph. A variant of the Hadwiger conjecture, stated by György Hajós, is that every n {\displaystyle n} -chromatic graph contains a subdivision...

graph minors and structure, the perfect graph conjecture, the Hadwiger conjecture, claw-free graphs, χ-boundedness, and the Erdős–Hajnal conjecture....

graphs are closed under the operation of taking minors and play a role in several other aspects of graph minor theory: linkless embedding, Hadwiger's...

k-chromatic graph has as a minor a k-vertex complete graph. The proof by Robertson, Seymour & Thomas (1993c) of the case k = 6 of Hadwiger's conjecture is sufficient...

in 1994 as co-author of a paper on the Hadwiger conjecture, and in 2009 for the proof of the strong perfect graph theorem. In 2011, he was awarded the Karel...

Wagner to show that the case k = 5 of the Hadwiger conjecture on the chromatic number of Kk-minor-free graphs is equivalent to the four color theorem....

theorem is equivalent to the case k = 5 of the Hadwiger conjecture. The chordal graphs are exactly the graphs that can be formed by clique-sums of cliques...

6 {\displaystyle K_{6}} -free case for which the Hadwiger conjecture relating graph coloring to graph minors is known to be true. In 1996, Robertson, Seymour...

are considered). In graph theory, isoperimetric inequalities are at the heart of the study of expander graphs, which are sparse graphs that have strong connectivity...

(graph theory) Fenchel's duality theorem (convex analysis) Fenchel–Moreau theorem (mathematical analysis) Hadwiger's theorem (geometry, measure theory)...

hull. Borsuk's conjecture - a conjecture about the number of pieces required to cover a body with a larger diameter. Solved by Hadwiger for the case of...

Robertson, Neil; Seymour, Paul; Thomas, Robin (1993). "Hadwiger's conjecture for K_6-free graphs". Combinatorica. 13 (3): 279–361. doi:10.1007/bf01202354...

In graph theory, a mathematical discipline, coloring refers to an assignment of colours or labels to vertices, edges and faces of a graph. Defective coloring...

Bollobás titled Hadwiger's conjecture is true for almost every graph. He authored over fifty academic papers in number theory and graph theory. Many of his...