the area of hyperbolic geometry, Hilbert's arithmetic of ends is a method for endowing a geometric set, the set of ideal points or "ends" of a hyperbolic...

Hilbert's arithmetic of ends Hilbert's paradox of the Grand Hotel Hilbert–Schmidt operator Hilbert–Smith conjecture Hilbert–Burch theorem Hilbert's irreducibility...

Hilbert's problems are 23 problems in mathematics published by German mathematician David Hilbert in 1900. They were all unsolved at the time, and several...

Hilbert–Serre theorem Hilbert–Smith conjecture Hilbert–Speiser theorem Hilbert–Waring theorem Hilbert's arithmetic of ends Hilbert's axioms Hilbert's basis theorem...

as a summary of Hilbert's beliefs on mathematics (its final six words, "Wir müssen wissen. Wir werden wissen!", were used as Hilbert's epitaph in 1943)...

Hilbert's paradox of the Grand Hotel (colloquial: Infinite Hotel Paradox or Hilbert's Hotel) is a thought experiment which illustrates a counterintuitive...

} Algebraic geometry Hyperbolic geometry Poincaré disc model Hilbert's arithmetic of ends Hartshorne, Robin (2000), Geometry: Euclid and beyond, Undergraduate...

Quotient ring construction Ward's twistor construction Hilbert symbol Hilbert's arithmetic of ends Colombeau's construction Vector bundle Integral monoid...

influential advocate, developing what became known as Hilbert's program to establish the consistency of mathematics through purely formal methods. The early...

the development of axiomatic frameworks for geometry, arithmetic, and analysis. In the early 20th century it was shaped by David Hilbert's program to prove...

a Hilbert system, sometimes called Hilbert calculus, Hilbert-style system, Hilbert-style proof system, Hilbert-style deductive system or Hilbert–Ackermann...

The axiomatization of arithmetic provided by Peano axioms is commonly called Peano arithmetic. The importance of formalizing arithmetic was not well appreciated...

primitive recursive arithmetic can be considered an upper bound on what Hilbert considered finitistic mathematics. As a result of Gödel's theorems, as...

logical formulas in order to reduce logic to arithmetic. The Entscheidungsproblem is related to Hilbert's tenth problem, which asks for an algorithm to...

set theory Hilbert–Ackermann system Entscheidungsproblem Ordinal notation Inverse Ackermann function 1928. "On Hilbert's construction of the real numbers"...

on Hilbert's second lecture on the foundations of mathematics in van Heijenoort 1967:484. Although Weyl the intuitionist believed that "Hilbert's view"...

established by David Hilbert, who initiated what is called Hilbert's program in the Foundations of Mathematics. The central idea of this program was that...

perhaps the creation of the term itself) owes itself to David Hilbert's attempt to secure the foundations of mathematics in the early part of the 20th century...

movement to mathematical logic, and opposition of David Hilbert's formalism movement (see: Brouwer–Hilbert controversy). Errett Bishop: American mathematician...

In number theory, an arithmetic, arithmetical, or number-theoretic function is generally any function whose domain is the set of positive integers and...

of its generalizations, along with Goldbach's conjecture and the twin prime conjecture, make up Hilbert's eighth problem in David Hilbert's list of twenty-three...

logic, Heyting arithmetic H A {\displaystyle {\mathsf {HA}}} is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It...

associated with it vanishes to order r at s = 1. Hilbert's tenth problem dealt with a more general type of equation, and in that case it was proven that...

if N is a positive integer and A=BN is definable in the arithmetic of rationals." Hilbert's tenth problem asks for an algorithm to determine whether...

In mathematics, Robinson arithmetic is a finitely axiomatized fragment of first-order Peano arithmetic (PA), first set out by Raphael M. Robinson in 1950...

who first presented it in 1926. Other modern axiomizations of Euclidean geometry are Hilbert's axioms (1899) and Birkhoff's axioms (1932). Using his axiom...

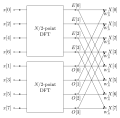
different FFT algorithms based on a wide range of published theories, from simple complex-number arithmetic to group theory and number theory. The best-known...

in SMT solvers; see, for instance, the decidability of Presburger arithmetic. SMT can be thought of as a constraint satisfaction problem and thus a certain...

is the Hilbert symbol of the completion at p. Hilbert's reciprocity law follows from the Artin reciprocity law and the definition of the Hilbert symbol...

results and more appears in Fried-Jarden's Field Arithmetic. Being Hilbertian is at the other end of the scale from being algebraically closed: the complex...