In mathematics, a homogeneous space is, very informally, a space that looks the same everywhere, as you move through it, with movement given by the action...

In mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G in which the stabilizer subgroup of every point...

codomain are vector spaces over a field F: a function f : V → W {\displaystyle f:V\to W} between two F-vector spaces is homogeneous of degree k {\displaystyle...

Thus any symmetric space is a reductive homogeneous space, but there are many reductive homogeneous spaces which are not symmetric spaces. The key feature...

{\mathcal {H}}} . Thus, anti-de Sitter is a reductive homogeneous space, and a non-Riemannian symmetric space. A d S n {\displaystyle \mathrm {AdS} _{n}} is...

Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's Elements, it was the three-dimensional...

space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to −1. It is homogeneous...

symmetry on a space, where the symmetries of the space were transformations forming a Lie group. The geometries of interest were homogeneous spaces G/H, but...

(orthonormal k-frames) are still homogeneous spaces for the orthogonal group, but not principal homogeneous spaces: any k-frame can be taken to any other...

variety (or simply flag variety) is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real...

space, so that P = Po. The homogeneous space GC / P has a complex structure, because P is a complex subgroup. The orbit in complex projective space is...

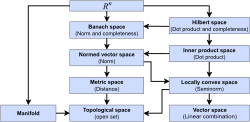
Function space G-space Geometric space Green space (topological space) Hardy space Hausdorff space Heisenberg space Hilbert space Homogeneous space Inner...

projective space being considered. For example, two homogeneous coordinates are required to specify a point on the projective line and three homogeneous coordinates...

{\displaystyle k} -frames) are still homogeneous spaces for the orthogonal group, but not principal homogeneous spaces: any k {\displaystyle k} -frame can...

timelike vector, so the homogeneous space SO+(1, 3) / SO(3) is the momentum space of a massive particle; geometrically, this space is none other than three-dimensional...

Lie groups and homogeneous spaces are defined intrinsically by using group actions to transport an inner product on a single tangent space to the entire...

system. The displacement vectors for that affine space are the solutions of the corresponding homogeneous linear system, which is a linear subspace. Linear...

vector space, in conjunction with an origin) often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space. In...

vector space. For a given n the elements of V n {\displaystyle V_{n}} are then called homogeneous elements of degree n. Graded vector spaces are common...

group G {\displaystyle G} is given, so that each fiber is a principal homogeneous space. The bundle is often specified along with the group by referring to...

Klein in his influential Erlangen program. More specifically, it is a homogeneous space X together with a transitive action on X by a Lie group G, which acts...

for homogeneous mixture and "non-uniform mixture" is another term for heterogeneous mixture. These terms are derived from the idea that a homogeneous mixture...

the dual space, a homogeneous space for SU(2) and SL(2,C). Irreducible compact Hermitian symmetric spaces are exactly the homogeneous spaces of simple...

{HP} ^{n}} and is a closed manifold of (real) dimension 4n. It is a homogeneous space for a Lie group action, in more than one way. The quaternionic projective...

The geometry of a n-dimensional space can also be described with Riemannian geometry. An isotropic and homogeneous space can be described by the metric:...

Cartan connections describe the geometry of manifolds modelled on homogeneous spaces. The theory of Cartan connections was developed by Élie Cartan, as...

deeper and more general). In other words, the "traditional spaces" are homogeneous spaces; but not for a uniquely determined group. Changing the group...

function defined by a homogeneous polynomial. A binary form is a form in two variables. A form is also a function defined on a vector space, which may be expressed...

MR0048803 "One-dimensional cohomology group of locally compact metrically homogeneous space." Duke Mathematical Journal 19, no. 2 (1952): 303–310. MR0047672 "Complex...

mean operator to homogeneous spaces. Instead of integrating over spheres, one integrates over generalized spheres: for a homogeneous space X = G/H, a generalized...