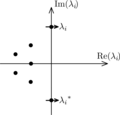
In mathematics, a Hurwitz-stable matrix, or more commonly simply Hurwitz matrix, is a square matrix whose eigenvalues all have strictly negative real...

referred to as Hurwitz matrices: A Hurwitz-stable matrix is a matrix whose eigenvalues all have negative real part. The Routh–Hurwitz matrix associated to...

mathematics, the Routh–Hurwitz matrix, or more commonly just Hurwitz matrix, corresponding to a polynomial is a particular matrix whose nonzero entries...

determinant Hurwitz-stable matrix Routh–Hurwitz matrix Hurwitz numbers Hurwitz polynomial Hurwitz problem Hurwitz quaternion order Hurwitz quaternion Hurwitz scheme...

these are referred to as stoquastic operators. Hurwitz-stable matrix M-matrix Metzler matrix P-matrix Bravyi, Sergey; DiVincenzo, David P.; Oliveira,...

mathematician Adolf Hurwitz independently proposed in 1895 to arrange the coefficients of the polynomial into a square matrix, called the Hurwitz matrix, and showed...

Routh–Hurwitz theorem provides an algorithm for determining if a given polynomial is Hurwitz stable, which is implemented in the Routh–Hurwitz and Liénard–Chipart...

differential equation M-matrix P-matrix Q-matrix, a specific kind of Metzler matrix Z-matrix Hurwitz-stable matrix Stochastic matrix Positive systems Berman...

its off-diagonal entries are less than or equal to zero. Hurwitz-stable matrix Metzler matrix David M. Young (2003). Iterative Solution of Large Linear...

\\|a_{ij}|&{\text{if }}i=j.\end{cases}}} Hurwitz-stable matrix P-matrix Perron–Frobenius theorem Z-matrix L-matrix M-matrix H-matrix (iterative method) Varga, Richard...

non-singular symmetric M-matrix is sometimes called a Stieltjes matrix. Hurwitz-stable matrix P-matrix Perron–Frobenius theorem Z-matrix H-matrix Fujimoto, Takao...

matrix A is Schur stable (resp. Hurwitz stable). Kreiss constant can be interpreted as a measure of normality of a matrix. In particular, for normal matrices...

is a M-matrix, A is a H-matrix. Invertible H-matrix guarantees convergence of Gauss–Seidel iterative methods. Hurwitz-stable matrix P-matrix Perron–Frobenius...

without solving the equation by using the Routh–Hurwitz stability criterion. The eigenvalues of a matrix are the roots of its characteristic polynomial...

left half-plane, and (r − σ)/2 lie in the open right half-plane; f is Hurwitz stable if and only if B n ( p , q ) {\displaystyle B_{n}(p,q)} is positive...

relation (zero matrix) as the zero, and the identity relation (identity matrix) as the unity. Central simple algebra Clifford algebra Hurwitz's theorem (normed...

Perron–Frobenius theorem. Doubly stochastic matrix Hurwitz-stable matrix Joel Lee Brenner Metzler matrix Muirhead's inequality Bendixson's inequality...

stability. If the Jacobian matrix of a dynamical system at a fixed point is Hurwitz, then the fixed point is asymptotically stable. Markus-Yamabe conjecture...

what is called Hurwitz determinants. Their definition is related to the associated Hurwitz matrix. Proposition 1. If all the Hurwitz determinants c i...

equations can be expressed as solutions of a matrix equation. Furthermore, if the matrix A {\displaystyle A} is "stable", the solution can also be expressed as...

and suppose A is Hurwitz (A,b) is controllable (A,c) is observable d > 0 and Φ ∈ (0,∞) then the system is globally asymptotically stable if there exists...

matrices used in mathematics, science and engineering. A matrix (plural matrices, or less commonly matrixes) is a rectangular array of numbers called entries...

Independently, Adolf Hurwitz analyzed system stability using differential equations in 1877, resulting in what is now known as the Routh–Hurwitz theorem. A notable...

minor of the Hurwitz matrix associated with f. Using the same notation as above, the Liénard–Chipart criterion is that f is Hurwitz stable if and only...

systole of hyperbolic surfaces reveals some interesting constants. Thus, Hurwitz surfaces Σg defined by a tower of principal congruence subgroups of the...

all normed division algebras over R {\displaystyle \mathbb {R} } . By Hurwitz's theorem they are the only ones; the sedenions, the next step in the Cayley–Dickson...

of spectral curves. It has applications in enumerative geometry, random matrix theory, mathematical physics, string theory, knot theory. The topological...

to zero asymptotically (i.e., when A − L C {\displaystyle A-LC} is a Hurwitz matrix). For a continuous-time linear system x ˙ = A x + B u , {\displaystyle...

1 ) {\displaystyle (n-1)\times (n-1)} matrix ( A 2 + L 2 A 12 ) {\displaystyle (A_{2}+L_{2}A_{12})} is Hurwitz (i.e., the real part of each of its eigenvalues...

can be represented as sums of four squares (proved using the norms of Hurwitz quaternions), and quadratic reciprocity. Chapter 3 concerns group theory...