In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables s with Re(s) > 1 and a ≠ 0,...
22 KB (4,190 words) - 03:21, 20 July 2025
zeta function of a variety Height zeta function of a variety Hurwitz zeta function, a generalization of the Riemann zeta function Igusa zeta function...
3 KB (379 words) - 14:35, 7 September 2023
Lerch transcendent (redirect from Hurwitz-Lerch zeta function)
mathematics, the Lerch transcendent, is a special function that generalizes the Hurwitz zeta function and the polylogarithm. It is named after Czech mathematician...
17 KB (3,654 words) - 17:40, 28 May 2025
L-functions may be written as a linear combination of the Hurwitz zeta function at rational values. Fixing an integer k ≥ 1, the Dirichlet L-functions for...
10 KB (1,633 words) - 13:22, 27 July 2025
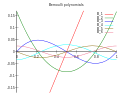
Bernoulli polynomials (redirect from Bernoulli function)
special functions and, in particular, the Riemann zeta function and the Hurwitz zeta function. They are an Appell sequence (i.e. a Sheffer sequence for...
19 KB (4,342 words) - 18:27, 2 June 2025
t\\&=(-1)^{m+1}m!\zeta (m+1,z)\end{aligned}}} where ζ ( s , q ) {\displaystyle \zeta (s,q)} is the Hurwitz zeta function. This expresses the polygamma function as the...
12 KB (2,386 words) - 18:50, 30 July 2025
(z)=\zeta _{H}'(0,z)-\zeta '(0),} where ζ H {\displaystyle \zeta _{H}} is the Hurwitz zeta function, ζ {\displaystyle \zeta } is the Riemann zeta function...
90 KB (13,545 words) - 04:27, 29 July 2025
Multiplication theorem (redirect from Periodic zeta function)
periodic zeta function occurs in the reflection formula for the Hurwitz zeta function, which is why the relation that it obeys, and the Hurwitz zeta relation...
10 KB (1,968 words) - 21:04, 21 May 2025
} making it a special case of the Hurwitz zeta function ψ 1 ( z ) = ζ ( 2 , z ) . {\displaystyle \psi _{1}(z)=\zeta (2,z).} Note that the last two formulas...
6 KB (1,125 words) - 12:09, 15 December 2024
Polylogarithm (redirect from De Jonquière's function)
polylogarithm function is equivalent to the Hurwitz zeta function — either function can be expressed in terms of the other — and both functions are special...
60 KB (10,143 words) - 16:31, 6 August 2025
Re(s) > 0. Alternatively, the following definition, in terms of the Hurwitz zeta function, is valid in the whole complex s-plane: β ( s ) = 4 − s ( ζ ( s...
8 KB (1,427 words) - 11:45, 24 June 2025
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined...
74 KB (10,595 words) - 15:06, 7 August 2025
The multiplication theorem for the Hurwitz zeta function ζ ( s , a ) = ∑ n = 0 ∞ ( n + a ) − s {\displaystyle \zeta (s,a)=\sum _{n=0}^{\infty }(n+a)^{-s}}...
7 KB (1,222 words) - 02:36, 4 May 2024
Riemann zeta function in mathematics The Hurwitz Zeta Function in mathematics The Weierstrass zeta-function The damping ratio of an oscillating system...
18 KB (2,220 words) - 19:47, 18 July 2025
first studied by Takuro Shintani (1976). They include Hurwitz zeta functions and Barnes zeta functions. Let P ( x ) {\displaystyle P(\mathbf {x} )} be a polynomial...
3 KB (481 words) - 17:57, 9 November 2020
{1}{k}}-\log n-\sum _{m=2}^{\infty }{\frac {\zeta (m,n+1)}{m}}\right),} where ζ(s, k) is the Hurwitz zeta function. The sum in this equation involves the harmonic...
71 KB (9,615 words) - 18:58, 30 July 2025
coefficients of higher order with Gn(1) = Gn, Γ is the gamma function and ζ is the Hurwitz zeta function. Similar series with the Cauchy numbers of the second...
36 KB (7,152 words) - 22:28, 2 August 2025
quaternion Hurwitz scheme Hurwitz surface Hurwitz zeta function Hurwitz's automorphisms theorem Hurwitz's theorem (complex analysis) Hurwitz's theorem (composition...
9 KB (984 words) - 12:29, 29 March 2025
} The Legendre chi function appears as the discrete Fourier transform, with respect to the order ν, of the Hurwitz zeta function, and also of the Euler...
3 KB (566 words) - 10:44, 15 June 2025
and the Riemann zeta function or the Hurwitz zeta function. Specifically, given a real number x, the rational zeta series for x is given by x = ∑ n = 2...
6 KB (1,434 words) - 16:12, 5 July 2024
Dirichlet beta function Dirichlet L-function Hurwitz zeta function Legendre chi function Lerch transcendent Polylogarithm and related functions: Incomplete...
10 KB (1,065 words) - 21:42, 29 July 2025
on the Hurwitz zeta function. The theta function was used by Jacobi to construct (in a form adapted to easy calculation) his elliptic functions as the...
70 KB (14,691 words) - 11:11, 4 August 2025
equation J. Horn: Horn hypergeometric series Adolf Hurwitz: Hurwitz zeta-function Hypergeometric function 2F1 Henry Jack (1917–1978) Dundee: Jack polynomial...
6 KB (614 words) - 14:03, 7 April 2025
{\displaystyle H_{n,m}=\zeta (m,1)-\zeta (m,n+1),} where ζ ( m , n ) {\displaystyle \zeta (m,n)} is the Hurwitz zeta function. This relationship is used...
40 KB (5,560 words) - 17:03, 31 July 2025
{\displaystyle N} approaches infinity, this becomes the Hurwitz zeta function ζ ( s , q ) {\displaystyle \zeta (s,q)} . For finite N {\displaystyle N} and q =...
7 KB (706 words) - 12:57, 25 July 2025
tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function. The Clausen function of order 2 – often referred...
31 KB (6,482 words) - 06:52, 8 August 2025
that paper, a slightly non-standard definition is used for the Hurwitz zeta function. Weisstein, Eric W. "Khinchin's constant". MathWorld. Ryll-Nardzewski...
12 KB (1,911 words) - 22:31, 2 August 2025
continuing ζ ( s ) {\displaystyle \zeta (s)} . Faulhaber's formula can be written in terms of the Hurwitz zeta function: ∑ k = 1 n k p = ζ ( − p ) − ζ (...
34 KB (8,401 words) - 13:42, 19 July 2025
{\bigl [}\zeta '(-1,z)-\zeta '(-1){\bigr ]}} where ζ′(z) denotes the derivative of the Riemann zeta function, ζ(a,z) denotes the Hurwitz zeta function and ζ...
5 KB (919 words) - 20:40, 27 May 2025
number Genocchi number Kummer's congruences Poly-Bernoulli number Hurwitz zeta function Euler summation Stirling polynomial Sums of powers Translation of...
93 KB (13,144 words) - 01:38, 9 July 2025