mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear...

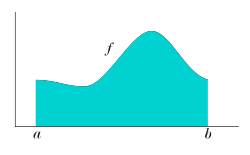
definite integral computes the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally...

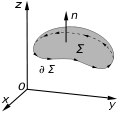
surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral...

In scientific visualization, line integral convolution (LIC) is a method to visualize a vector field (such as fluid motion) at high spatial resolutions...

method of complex analysis. One use for contour integrals is the evaluation of integrals along the real line that are not readily found by using only real...

surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analog of the line integral...

also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating...

In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that...

the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Wilhelm Leibniz, states that for an integral of the form...

calculus), a volume integral (∭) is an integral over a 3-dimensional domain; that is, it is a special case of multiple integrals. Volume integrals are especially...

real number line. ∫ 0 ∞ sin ⁡ x x d x = π 2 . {\displaystyle \int _{0}^{\infty }{\frac {\sin x}{x}}\,dx={\frac {\pi }{2}}.} This integral is not absolutely...

as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. It...

\limits _{D}f(x,y)\,dx\,dy.} The fundamental theorem of line integrals says that a line integral through a gradient field can be evaluated by evaluating...

property that its line integral is path independent; the choice of path between two points does not change the value of the line integral. Path independence...

vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary...

infinitesimals", it has two major branches, differential calculus and integral calculus. The former concerns instantaneous rates of change, and the slopes...

vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D (surface in R 2 {\displaystyle...

is Stokes' theorem, which relates the surface integral of the curl of a vector field to the line integral of the vector field around the boundary curve...

Augustin-Louis Cauchy (and Édouard Goursat), is an important statement about line integrals for holomorphic functions in the complex plane. Essentially, it says...

of differential and integral calculus extend naturally to vector fields. When a vector field represents force, the line integral of a vector field represents...

trigonometry, side lengths (Heron's formula), vectors, coordinates, line integrals, Pick's theorem, or other properties. Heron of Alexandria found what...

powerful tool to evaluate line integrals of analytic functions over closed curves; it can often be used to compute real integrals and infinite series as...

three-space to the line integral of the vector field over the surface boundary. The second fundamental theorem of calculus states that the integral of a function...

In mathematics, an integral transform is a type of transform that maps a function from its original function space into another function space via integration...

materials where μ0 is the magnetic constant. The integral form of the original circuital law is a line integral of the magnetic field around some closed curve...

Integration is the basic operation in integral calculus. While differentiation has straightforward rules by which the derivative of a complicated function...

In physics, circulation is the line integral of a vector field around a closed curve embedded in the field. In fluid dynamics, the field is the fluid...

Mathematically, this is expressed as the line integral of the electric field along that path. In electrostatics, this line integral is independent of the path taken...

Path integral may refer to: Line integral, the integral of a function along a curve Contour integral, the integral of a complex function along a curve...

line integral around the boundary curve ∂Σ, with the loop indicating the curve is closed. ∬ Σ {\displaystyle \iint _{\Sigma }} is a surface integral over...