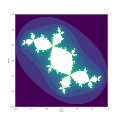
In mathematics, Lyapunov fractals (also known as Markus–Lyapunov fractals) are bifurcational fractals derived from an extension of the logistic map in...

Lyapunov equation Lyapunov exponent Lyapunov fractal Lyapunov function Lyapunov stability Lyapunov time Lyapunov's central limit theorem Lyapunov's condition...

following are named: Lyapunov dimension Lyapunov equation Lyapunov exponent Lyapunov function Lyapunov fractal Lyapunov stability Lyapunov's central limit theorem...

quasi-self-similar; also known as "orbit" fractals; e.g., the Mandelbrot set, Julia set, Burning Ship fractal, Nova fractal and Lyapunov fractal. The 2d vector fields that...

dimension Lévy C curve Lévy flight List of fractals by Hausdorff dimension Lorenz attractor Lyapunov fractal Mandelbrot set Menger sponge Minkowski–Bouligand...

Lyapunov equation, used in many branches of control theory, such as stability analysis and optimal control Lyapunov fractal, bifurcational fractals derived...

fractal dimension is a term invoked in the science of geometry to provide a rational statistical index of complexity detail in a pattern. A fractal pattern...

In mathematics, the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation...

Fractals "Julia set", Encyclopedia of Mathematics, EMS Press, 2001 [1994] Weisstein, Eric W. "Julia Set". MathWorld. Bourke, Paul. "Julia set fractal...

curve Lyapunov fractal Mandelbrot set - derived from complex quadratic map Menger sponge Newton fractal Nova fractal - derived from Newton fractal Quaternionic...

snowflake L-system Lévy C curve Feigenbaum attractor Lorenz attractor Lyapunov fractal Mandelbrot set Mandelbrot tree Mandelbulb Menger sponge Monkeys tree...

scale depending on the dynamics of the system, called the Lyapunov time. Some examples of Lyapunov times are: chaotic electrical circuits, about 1 millisecond;...

investigate some patterns physically. The technique arose out of and is used in fractal analysis. It also has application in related fields such as lacunarity...

commonly occurring fractals are described by the dyadic monoid; additional examples can be found in the article on de Rham curves. Other fractals possessing self-similarity...

L-systems, Lyapunov fractals, Newton fractals, Pickover stalks and Strange attractors. Many different features are included in fractal-generating software...

referred to a method of creating a fractal, using a polygon and an initial point selected at random inside it. The fractal is created by iteratively creating...

apparent that the decay rate, the fractal dimension and the Lyapunov exponents are all related. The large Lyapunov exponent, for instance, tells us how...

Aleksandr Lyapunov, founder of stability theory, author of the Lyapunov's central limit theorem, Lyapunov equation, Lyapunov fractal, Lyapunov time Leonty...

An ordinary fractal string Ω {\displaystyle \Omega } is a bounded, open subset of the real number line. Such a subset can be written as an at-most-countable...

simple way. Much greater fractal detail is revealed by plotting the Lyapunov exponent, as shown by the example below. The Lyapunov exponent is the error...

Aleksandr Lyapunov, founder of stability theory, author of the Lyapunov's central limit theorem, Lyapunov equation, Lyapunov fractal, Lyapunov time Yuri...

gauge integral; in fractal geometry, a synonym for dimension function; in control theory and dynamical systems, a synonym for Lyapunov candidate function;...

chaotic mixing is a process by which flow tracers develop into complex fractals under the action of a fluid flow. The flow is characterized by an exponential...

Aleksandr Lyapunov, founder of stability theory, author of the Lyapunov's central limit theorem, Lyapunov equation, Lyapunov fractal, Lyapunov time etc...

A Douady rabbit is a fractal derived from the Julia set of the function f c ( z ) = z 2 + c {\textstyle f_{c}(z)=z^{2}+c} , when parameter c {\displaystyle...

definition of the Lyapunov dimension. Especially for chaotic systems, the Kaplan–Yorke conjecture is a useful tool in order to estimate the fractal dimension...

Hénon strange attractor, or diverge to infinity. The Hénon attractor is a fractal, smooth in one direction and a Cantor set in another. Numerical estimates...

Lyapunov function is a function of the system f = f(x) whose existence in a system demonstrates stability. It is often useful to imagine a Lyapunov function...

sensitivity, can be quantitatively expressed by the Lyapunov exponent. For a one-dimensional map, the Lyapunov exponent λ can be calculated as follows: Here...

Digital morphogenesis Dual-phase evolution Emergence Evolution of complexity Fractal Game complexity Holism in science Law of Complexity/Consciousness Model...