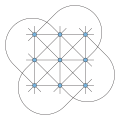
In geometry, the Möbius–Kantor configuration is a configuration consisting of eight points and eight lines, with three points on each line and three lines...
9 KB (1,011 words) - 01:54, 26 May 2025
called the Möbius–Kantor configuration. The Möbius–Kantor graph derives its name from being the Levi graph of the Möbius–Kantor configuration. It has one...
14 KB (1,599 words) - 20:42, 11 June 2025
Leipzig. Möbius died in Leipzig in 1868 at the age of 77. His son Theodor was a noted philologist. He is best known for his discovery of the Möbius strip...
8 KB (682 words) - 01:05, 16 June 2025
closely related configuration, the Möbius–Kantor configuration formed by two mutually inscribed quadrilaterals, has the Möbius–Kantor graph, a subgraph...
12 KB (1,346 words) - 18:15, 17 November 2023
Non-uniform structure 3. Generalized quadrangle 4. Möbius–Kantor configuration 5. Pappus configuration An incidence structure is uniform if each line is...
19 KB (2,595 words) - 15:39, 27 December 2024
edges. Coxeter named it a Möbius–Kantor polygon for sharing the complex configuration structure as the Möbius–Kantor configuration, (83). Discovered by G...
5 KB (459 words) - 19:13, 9 June 2025
Dual configuration The dual configuration, (123 94), points indexed 1...12 can have configuration table: Möbius–Kantor configuration Removing any...
13 KB (1,386 words) - 06:40, 9 May 2025
This configuration exists as an abstract incidence geometry, but cannot be constructed in the Euclidean plane. (83), the Möbius–Kantor configuration. This...
16 KB (1,692 words) - 21:11, 5 August 2025
Levi graph (category Configurations (geometry))
and is 3-regular with 14 vertices. The Möbius–Kantor graph is the Levi graph of the Möbius–Kantor configuration, a system of 8 points and 8 lines that...
6 KB (601 words) - 16:47, 27 December 2024
Austro-Hungarian Empire. He is known for the Möbius–Kantor configuration and the Möbius-Kantor graph. Kantor studied mathematics and physics at the Technische...
4 KB (399 words) - 05:40, 11 May 2025
Incidence geometry (section Möbius planes)
other points on them) produces the (83) Möbius–Kantor configuration. Given an integer α ≥ 1, a tactical configuration satisfying: For every anti-flag (B,...
27 KB (3,319 words) - 17:55, 18 May 2025
realization; the Möbius–Kantor configuration of eight points and eight lines does not. It is known that every regular configuration with three lines per...
14 KB (1,922 words) - 06:56, 4 August 2025
definitions exist only for the regular complex polytopes, which are configurations. The regular complex polytopes have been completely characterized, and...
154 KB (6,983 words) - 12:31, 4 August 2025
graphs are the cubical graph G(4, 1), the Petersen graph G(5, 2), the Möbius–Kantor graph G(8, 3), the dodecahedral graph G(10, 2) and the Nauru graph G(12...
10 KB (1,203 words) - 11:19, 3 August 2024
duopyramid G4=G(1,1,2) 3[3]3 <2,3,3> 24 6 3(24)3 3{3}3 8 8 3{} Möbius–Kantor configuration self-dual, same as R 4 {\displaystyle \mathbb {R} ^{4}} representation...
37 KB (1,846 words) - 08:53, 28 November 2024
{\displaystyle G(n,1)} the Dürer graph G ( 6 , 2 ) {\displaystyle G(6,2)} , the Möbius-Kantor graph G ( 8 , 3 ) {\displaystyle G(8,3)} , the dodecahedron G ( 10 ...
24 KB (2,993 words) - 04:57, 12 April 2025
hyperplanes of symmetry passing through the center yield complex 3{4}3 Möbius–Kantor polygons. The root vectors of simple Lie group E8 are represented by...
15 KB (2,028 words) - 13:54, 4 August 2025
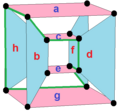
16-cell (section As a configuration)
duoprism, the 16-cell can be seen as its dual, a 4-4 duopyramid. The Möbius–Kantor polygon is a regular complex polygon 3{3}3, , in C 2 {\displaystyle...
61 KB (7,127 words) - 23:26, 1 August 2025
G(4,1)} , the Petersen graph G ( 5 , 2 ) {\displaystyle G(5,2)} , the Möbius–Kantor graph G ( 8 , 3 ) {\displaystyle G(8,3)} , the dodecahedral graph G...
11 KB (1,378 words) - 20:54, 8 February 2025
G(n,1)} , the Dürer graph G ( 6 , 2 ) {\displaystyle G(6,2)} , the Möbius-Kantor graph G ( 8 , 3 ) {\displaystyle G(8,3)} , the dodecahedron G ( 10 ...
12 KB (1,598 words) - 05:22, 15 July 2025
Amer. Math. Soc. 81 (3): 536–538. doi:10.1090/s0002-9904-1975-13731-1. Kantor, William M. (1981). "Review of Permutation groups and combinatorial structures...
12 KB (1,326 words) - 08:55, 27 May 2025
Servatius, Brigitte (2013), "2.3.2 Cubic graphs and LCF notation", Configurations from a Graphical Viewpoint, Springer, p. 32, ISBN 9780817683641. Frucht...
11 KB (635 words) - 17:43, 9 May 2025