In mathematics, the qualifier pointwise is used to indicate that a certain property is defined by considering each value f ( x ) {\displaystyle f(x)}...

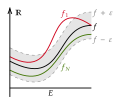
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function. It is weaker than...

In statistics, probability theory and information theory, pointwise mutual information (PMI), or point mutual information, is a measure of association...

uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions ( f n ) {\displaystyle (f_{n})} converges...

operators (and thus bounded operators) whose domain is a Banach space, pointwise boundedness is equivalent to uniform boundedness in operator norm. The...

equicontinuous and converges pointwise to a function (not necessarily continuous a-priori). In particular, the limit of an equicontinuous pointwise convergent sequence...

is almost everywhere pointwise convergent to a function then the sequence converges in L 1 {\displaystyle L_{1}} to its pointwise limit, and in particular...

provides an analogous example showing that polyhedral surfaces that converge pointwise to a curved surface do not necessarily converge to its area, even when...

convergence in distribution of the sequence of random variables with pointwise convergence of their characteristic functions. This theorem is the basis...

producing bounds on the CDF, we must differentiate between pointwise and simultaneous bands. A pointwise CDF bound is one which only guarantees their Coverage...

is a result that says, heuristically, whenever certain curvatures are pointwise constant then they are forced to be globally constant. The proof is essentially...

set X into a vector space has a natural vector space structure given by pointwise addition and scalar multiplication. In other scenarios, the function space...

{\tfrac {n}{P}}x}\,dx.} The series does not necessarily converge (in the pointwise sense) and, even if it does, it is not necessarily equal to s ( x ) {\displaystyle...

to occur. Determination of convergence requires the comprehension of pointwise convergence, uniform convergence, absolute convergence, Lp spaces, summability...

turned into a vector space under the operations of pointwise addition of functions and pointwise scalar multiplication. All sequence spaces are linear...

Riemann curvature tensor. A manifold M n {\displaystyle M^{n}} is called pointwise Osserman if, for every p ∈ M n {\displaystyle p\in M^{n}} , the spectrum...

-topology on F {\displaystyle F} is called the topology of pointwise convergence. The topology of pointwise convergence on F {\displaystyle F} is identical to...

a group of loops in a topological group G with multiplication defined pointwise. In its most general form a loop group is a group of continuous mappings...

In mathematics, the lower envelope or pointwise minimum of a finite set of functions is the pointwise minimum of the functions, the function whose value...

Then: the sequence { g n ( x ) } n {\displaystyle \{g_{n}(x)\}_{n}} is pointwise non-decreasing at any x and g n ≤ f n {\displaystyle g_{n}\leq f_{n}}...

on the circle, Hεf converges uniformly to Hf, so in particular pointwise. The pointwise limit is a Cauchy principal value, written H f = P . V . 1 π ∫...

called pointwise limit, denoted x n , m → y m pointwise {\displaystyle x_{n,m}\to y_{m}\quad {\text{pointwise}}} , or lim n → ∞ x n , m = y m pointwise {\displaystyle...

(see microcontinuity). The formal definition and the distinction between pointwise continuity and uniform continuity were first given by Bolzano in the 1830s...

well. This theorem does not hold if uniform convergence is replaced by pointwise convergence. For example, let ƒn : [0, 1] → R be the sequence of functions...

In natural language processing and information retrieval, cluster labeling is the problem of picking descriptive, human-readable labels for the clusters...

theorem says that if a monotone sequence of continuous functions converges pointwise on a compact space and if the limit function is also continuous, then...

relativity, a frame field (also called a tetrad or vierbein) is a set of four pointwise-orthonormal vector fields, one timelike and three spacelike, defined on...

fundamental result in mathematical analysis establishing the (Lebesgue) pointwise almost everywhere convergence of Fourier series of L2 functions, proved...

Egorov's theorem establishes a condition for the uniform convergence of a pointwise convergent sequence of measurable functions. It is also named Severini–Egoroff...

the sequence of corresponding characteristic functions {φn} converges pointwise to the characteristic function φ of X. Convergence in distribution is...