and computational algebra, Pollard's kangaroo algorithm (also Pollard's lambda algorithm, see Naming below) is an algorithm for solving the discrete logarithm...

Pollard's rho algorithm is an algorithm for integer factorization. It was invented by John Pollard in 1975. It uses only a small amount of space, and its...

Several algorithms created by British mathematician John Pollard: Pollard's kangaroo algorithm Pollard's p − 1 algorithm Pollard's rho algorithm Pollard (coin)...

calculus algorithm Number field sieve Pohlig–Hellman algorithm Pollard's rho algorithm for logarithms Pollard's kangaroo algorithm (aka Pollard's lambda...

logarithm of 2 Neper Offset logarithmic integral pH Pollard's kangaroo algorithm Pollard's rho algorithm for logarithms Polylogarithm Polylogarithmic function...

division algorithm: for polynomials in several indeterminates Pollard's kangaroo algorithm (also known as Pollard's lambda algorithm): an algorithm for solving...

character NTLM passwords. A5/1 Brute-force attack DistrRTgen Pollard's kangaroo algorithm Oechslin, P. (2003). "Making a Faster Cryptanalytic Time-Memory...

Pollard's rho algorithm for logarithms is an algorithm introduced by John Pollard in 1978 to solve the discrete logarithm problem, analogous to Pollard's...

Pollard's p − 1 algorithm is a number theoretic integer factorization algorithm, invented by John Pollard in 1974. It is a special-purpose algorithm, meaning...

division algorithm: for polynomials in several indeterminates Pollard's kangaroo algorithm (also known as Pollard's lambda algorithm): an algorithm for solving...

where the discrete logarithm solution lies unlike with the Pollard's rho or Pollard's kangaroo. Input: Discrete logarithm generator g {\displaystyle g}...

perform exponentiation in a quadratic field. It is analogous to Pollard's p − 1 algorithm. Choose some integer A greater than 2 which characterizes the...

improved by others. His discrete logarithm algorithms include the rho algorithm for logarithms and the kangaroo algorithm. He received the RSA Award for Excellence...

Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor...

number-theoretic algorithms are based on cycle detection, including Pollard's rho algorithm for integer factorization and his related kangaroo algorithm for the...

primality test and cyclotomic AKS test) is a deterministic primality-proving algorithm created and published by Manindra Agrawal, Neeraj Kayal, and Nitin Saxena...

Brent. Algebraic-group factorization algorithms, among which are Pollard's p − 1 algorithm, Williams' p + 1 algorithm, and Lenstra elliptic curve factorization...

first step of the algorithm. Doing so increases the running time, which then is O(n/m). Alternatively one can use Pollard's rho algorithm for logarithms...

Ergodic theory Geometric distribution Overlapping instructions Pollard's kangaroo algorithm Random walk Self-synchronizing code According to Diaconis & Graham...

essential step in several integer factorization algorithms, such as Pollard's rho algorithm, Shor's algorithm, Dixon's factorization method and the Lenstra...

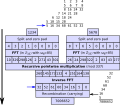
multiplication algorithm is an algorithm (or method) to multiply two numbers. Depending on the size of the numbers, different algorithms are more efficient...

In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking...

The Karatsuba algorithm is a fast multiplication algorithm for integers. It was discovered by Anatoly Karatsuba in 1960 and published in 1962. It is a...

|a|. This case is important as the terminating step of the Euclidean algorithm. The above definition is unsuitable for defining gcd(0, 0), since there...

ISBN 978-3-319-78555-4. Pons, Jean-Luc; Zieniewicz, Aleksander (17 January 2022). "Pollard's kangaroo for SECPK1". GitHub. Computations of discrete logarithms sorted by...

The Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen...

In computational number theory, Cipolla's algorithm is a technique for solving a congruence of the form x 2 ≡ n ( mod p ) , {\displaystyle x^{2}\equiv...

and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common...

modular multiplicative inverse d of b modulo m using the extended Euclidean algorithm. That is: c = be mod m = d−e mod m, where e < 0 and b ⋅ d ≡ 1 (mod m)...

The Tonelli–Shanks algorithm (referred to by Shanks as the RESSOL algorithm) is used in modular arithmetic to solve for r in a congruence of the form r2...