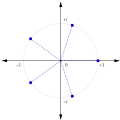
In finite field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite field GF(pm). This...

primitive polynomial may refer to: Primitive polynomial (field theory), a minimal polynomial of an extension of finite fields Primitive polynomial (ring...

In field theory, a primitive element of a finite field GF(q) is a generator of the multiplicative group of the field. In other words, α ∈ GF(q) is called...

In field theory, a simple extension is a field extension that is generated by the adjunction of a single element, called a primitive element. Simple extensions...

coefficients. The primitive part of such a polynomial is the quotient of the polynomial by its content. Thus a polynomial is the product of its primitive part and...

greater than 1 are never primitive. Even parity polynomial marked as primitive in this table represent a primitive polynomial multiplied by ( x + 1 ) {\displaystyle...

the theory of factorization and greatest common divisors of such polynomials. Gauss's lemma asserts that the product of two primitive polynomials is primitive...

(X6 + X + 1). In fact, this generator is a primitive element, and this polynomial is the irreducible polynomial that produces the easiest Euclidean division...

is called a primitive polynomial if all of its roots are primitive elements of GF(qn). In the polynomial representation of the finite field, this implies...

In mathematics, an all one polynomial (AOP) is a polynomial in which all coefficients are one. Over the finite field of order two, conditions for the...

Field theory is the branch of mathematics in which fields are studied. This is a glossary of some terms of the subject. (See field theory (physics) for...

In field theory, the primitive element theorem states that every finite separable field extension is simple, i.e. generated by a single element. This theorem...

theorem, which asserts that a general polynomial of degree at least five cannot be solved by radicals. Galois theory has been used to solve classic problems...

field theory, a branch of mathematics, the minimal polynomial of an element α of an extension field of a field is, roughly speaking, the polynomial of...

complex numbers. Field extensions are fundamental in algebraic number theory, and in the study of polynomial roots through Galois theory, and are widely...

as the monic polynomial with integer coefficients that is the minimal polynomial over the field of the rational numbers of any primitive nth-root of unity...

up primitive in Wiktionary, the free dictionary. Primitive may refer to: Primitive element (field theory) Primitive element (finite field) Primitive cell...

algebra, factorization of polynomials or polynomial factorization expresses a polynomial with coefficients in a given field or in the integers as the...

derivative of polynomials forms a differential field. These fields are central to differential Galois theory, a variant of Galois theory dealing with linear...

polynomials over a field the polynomial GCD may be computed, like for the integer GCD, by the Euclidean algorithm using long division. The polynomial...

extensions and their relationship to the polynomials that give rise to them via Galois groups is called Galois theory, so named in honor of Évariste Galois...

In algebra, a monic polynomial is a non-zero univariate polynomial (that is, a polynomial in a single variable) in which the leading coefficient (the...

In mathematics, the Conway polynomial Cp,n for the finite field Fpn is a particular irreducible polynomial of degree n over Fp that can be used to define...

exponentiation) p(a) ≡ p(b) (mod m), for any polynomial p(x) with integer coefficients (compatibility with polynomial evaluation) If a ≡ b (mod m), then it is...

reversing its coefficients, and (being primitive) is therefore irreducible in Z[x]. An important class of polynomials whose irreducibility can be established...

any intermediate field between L {\displaystyle L} and K {\displaystyle K} , and let g {\displaystyle g} be the minimal polynomial of α {\displaystyle...

conveniently by means of field theory, as the transformation on minimal polynomials implied by a different choice of primitive element. This is the most...

primitive.) This implies that z, z2, ..., zn−1, zn = z0 = 1 are all of the nth roots of unity, since an nth-degree polynomial equation over a field (in...

generating set of an ideal in a polynomial ring K [ x 1 , … , x n ] {\displaystyle K[x_{1},\ldots ,x_{n}]} over a field K {\displaystyle K} . A Gröbner...

solution of the roots of unity polynomial equations Xm − 1 in the ring Z {\displaystyle \mathbb {Z} } n), or simply a primitive element of Z {\displaystyle...