In mathematics, a real number is a number that can be used to measure a continuous one-dimensional quantity such as a duration or temperature. Here, continuous...
61 KB (8,195 words) - 16:29, 17 April 2025
π: Every point of the number line corresponds to a unique real number, and every real number to a unique point. Using a number line, numerical concepts...
20 KB (2,549 words) - 17:44, 4 April 2025
Informally, a definable real number is a real number that can be uniquely specified by its description. The description may be expressed as a construction...
11 KB (1,502 words) - 02:55, 9 April 2024
In mathematics, the extended real number system is obtained from the real number system R {\displaystyle \mathbb {R} } by adding two elements denoted...
15 KB (2,205 words) - 20:35, 16 December 2024
numbers are an extension of the real numbers to include certain classes of infinite and infinitesimal numbers. A hyperreal number x {\displaystyle x} is said...
33 KB (4,924 words) - 08:45, 23 June 2025
recursive numbers, effective numbers, computable reals, or recursive reals. The concept of a computable real number was introduced by Émile Borel in 1912, using...
24 KB (3,270 words) - 00:15, 16 June 2025
In number theory, a number field F is called totally real if for each embedding of F into the complex numbers the image lies inside the real numbers....
2 KB (260 words) - 12:56, 10 December 2021
bi, the real number a is called the real part and b is called the imaginary part. If the real part of a complex number is 0, then the number is called...
67 KB (8,504 words) - 16:14, 25 June 2025
In mathematics, a transcendental number is a real or complex number that is not algebraic: that is, not the root of a non-zero polynomial with integer...
52 KB (6,815 words) - 10:41, 22 June 2025
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted i, called the imaginary...
91 KB (12,021 words) - 17:33, 29 May 2025
Decimal (redirect from Decimal approximation of a real number)
sometimes is called a fractional number. Decimals are commonly used to approximate real numbers. By increasing the number of digits after the decimal separator...
42 KB (5,080 words) - 17:13, 27 May 2025
rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits...
24 KB (3,391 words) - 07:07, 16 June 2025
In mathematics, there are several equivalent ways of defining the real numbers. One of them is that they form a complete ordered field that does not contain...
31 KB (4,189 words) - 22:18, 29 January 2025
imaginary number is the product of a real number and the imaginary unit i, which is defined by its property i2 = −1. The square of an imaginary number bi is...
12 KB (1,347 words) - 02:23, 8 May 2025
property of the real numbers that, intuitively, implies that there are no "gaps" (in Dedekind's terminology) or "missing points" in the real number line. This...
11 KB (1,511 words) - 14:38, 6 June 2025
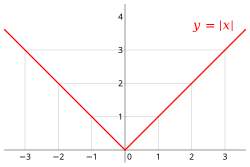
Absolute value (redirect from Absolute value of a real number)
In mathematics, the absolute value or modulus of a real number x {\displaystyle x} , denoted | x | {\displaystyle |x|} , is the non-negative value of...
27 KB (3,477 words) - 09:59, 20 April 2025
are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the case of irrational...
40 KB (5,309 words) - 18:34, 23 June 2025
Diophantine approximation (redirect from Metrical number theory)
In number theory, the study of Diophantine approximation deals with the approximation of real numbers by rational numbers. It is named after Diophantus...
30 KB (4,072 words) - 21:09, 22 May 2025
Sign (mathematics) (redirect from Nonnegative number)
In mathematics, the sign of a real number is its property of being either positive, negative, or 0. Depending on local conventions, zero may be considered...
29 KB (2,740 words) - 09:55, 12 April 2025
mathematics, hypercomplex number is a traditional term for an element of a finite-dimensional unital algebra over the field of real numbers. The study of...
27 KB (3,215 words) - 22:17, 5 June 2025
while infinity is commonly defined either as an extreme limit of the real number line (applied to a function or sequence that "diverges to infinity" or...
17 KB (2,453 words) - 10:45, 21 June 2025
positive real axis, and is usually drawn as a horizontal ray. This ray is used as reference in the polar form of a complex number. The real positive axis...
9 KB (1,428 words) - 02:44, 30 March 2025
values 0, 1 and ∞. The projectively extended real number line is distinct from the affinely extended real number line, in which +∞ and −∞ are distinct. Unlike...
20 KB (3,064 words) - 01:21, 19 May 2025
functions. The theorems of real analysis rely on the properties of the (established) real number system. The real number system consists of an uncountable...
49 KB (7,670 words) - 19:52, 25 June 2025
In mathematics, a negative number is the opposite of a positive real number. Equivalently, a negative number is a real number that is less than zero. Negative...
38 KB (4,634 words) - 08:28, 29 April 2025
Arithmetic (section Real number arithmetic)
integers. Rational number arithmetic involves operations on fractions of integers. Real number arithmetic is about calculations with real numbers, which include...
165 KB (16,396 words) - 04:14, 2 June 2025
Imaginary unit (redirect from I (number))
imaginary number (i) is a mathematical constant that is a solution to the quadratic equation x2 + 1 = 0. Although there is no real number with this property...
30 KB (4,171 words) - 09:38, 24 June 2025
In number theory, a Liouville number is a real number x {\displaystyle x} with the property that, for every positive integer n {\displaystyle n} , there...
20 KB (4,187 words) - 13:26, 8 June 2025
A real data type is a data type used in a computer program to represent an approximation of a real number. Because the real numbers are not countable...
3 KB (308 words) - 15:49, 11 February 2024
Homogeneous function (redirect from Real homogeneity)
0 , {\displaystyle s>0,} and allowing any real number k as a degree of homogeneity. Every homogeneous real function is positively homogeneous. The converse...
26 KB (4,588 words) - 16:08, 7 January 2025