In mathematics, the study of special values of L-functions is a subfield of number theory devoted to generalising formulae such as the Leibniz formula...

interpolation of special values of L-functions. For example, Kubota–Leopoldt used Kummer's congruences for Bernoulli numbers to construct a p-adic L-function, the...

conjecture Special values of L-functions Explicit formulae for L-functions Shimizu L-function Steuding, Jörn (June 2005). "An Introduction to the Theory of L-functions"...

(1984) had proposed a set of far-reaching conjectures describing the special values of L-functions, i.e., the values of L-functions at integers. In very rough...

University of California, San Diego. His research interests are in algebraic number theory, and in particular, in special values of L-functions. The son of historian...

Special functions are particular mathematical functions that have more or less established names and notations due to their importance in mathematical...

{r}{k}}\right).} Generalized Riemann hypothesis L-function Modularity theorem Artin conjecture Special values of L-functions Apostol 1976, Theorem 11.7 Davenport...

elliptic functions and approximately equal to 2.62205755. It also appears in evaluation of the gamma and beta function at certain rational values. The symbol...

conjectures for special values of L-functions in 1990. Bloch is a member of the U.S. National Academy of Sciences and a Fellow of the American Academy of Arts and...

is used to formulate Beilinson conjectures on special values of L-functions. There is an extension of Deligne-cohomology defined for any symmetric spectrum...

special values of L-functions. The lower K-groups were discovered first, in the sense that adequate descriptions of these groups in terms of other algebraic...

intersection theory, algebraic dynamics, Diophantine equations and special values of L-functions. Yuan is from Macheng, Huanggang, Hubei province, and graduated...

Real-valued functions of a real variable (commonly called real functions) and real-valued functions of several real variables are the main object of study...

adding and subtracting logarithmic values instead of multiplying and dividing very large values. It is often defined as l o g Γ ⁡ ( z ) = − γ z − log ⁡ z...

function, such as Deligne's conjecture on special values of L-functions, the Beilinson conjecture, and the Bloch–Kato conjecture (on special values of...

elliptic curves to special values of L-functions, which was developed with Bryan Birch during the first half of the 1960s with the help of machine computation...

equal to L. The limit in Euclidean space is a direct generalization of limits to vector-valued functions. For example, we may consider a function f : S ×...

{\displaystyle f(x)={\frac {L}{1+e^{-k(x-x_{0})}}}} where L {\displaystyle L} is the carrying capacity, the supremum of the values of the function; k {\displaystyle...

known, although these values are thought to be related to the algebraic K-theory of the integers; see Special values of L-functions. For nonpositive integers...

In mathematics, the L-functions of number theory are expected to have several characteristic properties, one of which is that they satisfy certain functional...

quadratic form. It is a special case of a Hasse–Weil L-function. The natural definition of L(E, s) only converges for values of s in the complex plane...

In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems...

elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum, as well as in the design of electronic...

Deligne conjecture on special values of L-functions is a formulation of the hope for algebraicity of L(n) where L is an L-function and n is an integer in...

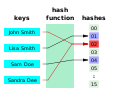
A hash function is any function that can be used to map data of arbitrary size to fixed-size values, though there are some hash functions that support...

sign function or signum function (from signum, Latin for "sign") is a function that has the value −1, +1 or 0 according to whether the sign of a given...

the two values y = W0(x) and y = W−1(x) if −⁠1/e⁠ ≤ x < 0. The Lambert W function's branches cannot be expressed in terms of elementary functions. It is...

} Zeta functions include: Airy zeta function, related to the zeros of the Airy function Arakawa–Kaneko zeta function Arithmetic zeta function Artin–Mazur...

conjecture on special values of L-functions. The Dirichlet regulator map (used in the proof of Dirichlet's unit theorem) for the ring of integers O F {\displaystyle...

quantile function. Statistical applications of quantile functions are discussed extensively by Gilchrist. Monte-Carlo simulations employ quantile functions to...