the Szilassi polyhedron is a nonconvex polyhedron, topologically a torus, with seven hexagonal faces. The tetrahedron and the Szilassi polyhedron are...

is seven. The Császár polyhedron has the fewest possible vertices of any embedded toroidal polyhedron, and the Szilassi polyhedron has the fewest possible...

polyhedron is named after Hungarian topologist Ákos Császár, who discovered it in 1949. The dual to the Császár polyhedron, the Szilassi polyhedron,...

is the Szilassi polyhedron, which has the geometrically ralizes the Heawood map. For every convex polyhedron, there exists a dual polyhedron having faces...

was soon dubbed the Szilassi polyhedron. This is mathematically significant because the tetrahedron and the Szilassi polyhedron are the only two known...

alongside other uniform prisms, has 14 faces. The Szilassi polyhedron and its dual, the Császár polyhedron, are the simplest toroidal polyhedra; they have...

upper bound of 7 is sharp: certain toroidal polyhedra such as the Szilassi polyhedron require seven colors. A Möbius strip requires six colors (Tietze...

square hosohedron is another polyhedron with four faces, but it does not have triangular faces. The Szilassi polyhedron and the tetrahedron are the only...

and so on. One particularly interesting example is the Szilassi polyhedron, a Toroidal polyhedron with 7 non-convex six sided faces. Frank Chester. "The...

maximal. The map can be faithfully realized as the Szilassi polyhedron, the only known polyhedron apart from the tetrahedron such that every pair of faces...

Rhombohedron Scalenohedron Schönhardt polyhedron Square bifrustum Square truncated trapezohedron Szilassi polyhedron Tetradecahedron Tetradyakis hexahedron...

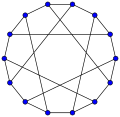
forms an embedding of the Heawood graph onto the torus. Grünbaum, Branko; Szilassi, Lajos (2009), "Geometric Realizations of Special Toroidal Complexes",...

Rhombohedron Scalenohedron Schönhardt polyhedron Square bifrustum Square truncated trapezohedron Szilassi polyhedron Tetradecahedron Tetradyakis hexahedron...

Szemerédi's theorem according to ergodic theory. Lajos Szilassi discovers the Szilassi polyhedron. Joel L. Weiner describes a version of the tennis ball...

triacontahedron. The second edition also includes the Császár polyhedron and Szilassi polyhedron, toroidal polyhedra with non-regular faces but with pairwise...

Differential Geometry. 6 (3): 271–283. doi:10.4310/jdg/1214430493. MR 0314057. Szilassi, Lajos (2008). "A polyhedral model in Euclidean 3-space of the six-pentagon...