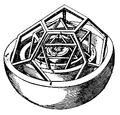
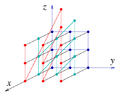
geometry and mathematical group theory, a unimodular lattice is an integral lattice of determinant 1 or −1. For a lattice in n-dimensional Euclidean space, this...

mathematics, unimodular may refer to any of the following: Unimodular lattice Unimodular matrix Unimodular polynomial matrix Unimodular form Unimodular group...

mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8. The name...

In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space which is one of the best models for the kissing...

In mathematics, a Niemeier lattice is one of the 24 positive definite even unimodular lattices of rank 24, which were classified by Hans-Volker Niemeier (1973)...

constant Lattice-based cryptography Lattice graph Lattice (module) Lattice (order) Mahler's compactness theorem Reciprocal lattice Unimodular lattice "Symmetry...

only one even unimodular lattice in 15 dimensions or less — the E8 lattice. Up to dimension 24, there is only one even unimodular lattice without roots...

to find unimodular groups without lattices, for example certain nilpotent Lie groups as explained below. A stronger condition than unimodularity is simplicity...

unimodular matrix used (possibly implicitly) in lattice reduction and in the Hermite normal form of matrices. The Kronecker product of two unimodular...

of a root lattice. The integer lattice is an odd unimodular lattice. The automorphism group (or group of congruences) of the integer lattice consists of...

function of a lattice is then a holomorphic function on the upper half-plane. Furthermore, the theta function of an even unimodular lattice of rank n is...

positive unimodular lattice I I 25 , 1 {\displaystyle \mathrm {II_{25,1}} } in twenty-six dimensions is constructed from the Leech lattice in twenty-four...

160,000,000 even unimodular lattices (of determinants 1 or −1); which is a marked increase from the twenty-four such Niemeier lattices that exists in twenty-four...

identically zero. II. Theta functions of even unimodular lattices An even unimodular lattice L in Rn is a lattice generated by n vectors forming the columns...

is the odd unimodular lattice I1,9−d, except when the surface is a product of 2 lines when the Picard group is the even unimodular lattice II1,1.When...

{R} ^{n})} (L1 for L1 space) and Λ {\displaystyle \Lambda } is a unimodular lattice in R n {\displaystyle \mathbb {R} ^{n}} . Then the periodization of...

In mathematics, II25,1 is the even 26-dimensional Lorentzian unimodular lattice. It has several unusual properties, arising from Conway's discovery that...

12}={1 \over 696729600}.} There is exactly one even unimodular lattice of dimension 8, the E8 lattice, whose automorphism group is the Weyl group of E8...

connections. There are 26 sporadic groups. The 26-dimensional Lorentzian unimodular lattice II25,1 plays a significant role in sphere packing problems and the...

with values in the integers, known as the K3 lattice. This is isomorphic to the even unimodular lattice II 3 , 19 {\displaystyle \operatorname {II} _{3...

an integral lattice, det ( L ) 2 = | L ∗ / L | {\textstyle {\text{det}}(L)^{2}=|L^{*}/L|} . An integral lattice is said to be unimodular if L = L ∗ {\textstyle...

second cohomology group H2(X, Z) is isomorphic to the unique even unimodular lattice II3,19 of dimension 22 and signature −16. Hodge diamond: Examples:...

cohomology group H2(X, Z) is isomorphic to the sum of the unique even unimodular lattice II1,9 of dimension 10 and signature -8 and a group of order 2. Hodge...

Picard group is the odd unimodular lattice I1,n, except for the Hirzebruch surfaces Σ2m when it is the even unimodular lattice II1,1. Guido Castelnuovo...

signature. This can be used to compute its intersection form as a unimodular lattice since it has dim ⁡ ( H 2 ( X ) ) = 22 {\displaystyle \operatorname...

a lattice in R8 naturally called the E8 root lattice. This lattice is rather remarkable in that it is the only (nontrivial) even, unimodular lattice with...

their intersection forms have the same rank, signature, and parity. Unimodular lattice Donaldson theory Yang–Mills equations Rokhlin's theorem Donaldson...

the intersection form is even. By a theorem of Cahit Arf, any even unimodular lattice has signature divisible by 8, so Rokhlin's theorem forces one extra...

is unimodular and G\X is finite. Also equivalent is the existence of a uniform X-lattice in G. Bass, Hyman; Lubotzky, Alexander (2001), Tree Lattices, Progress...

mathematician who in 1973 classified the Niemeier lattices, the even positive definite unimodular lattices in 24 dimensions. Hans-Volker Niemeier at the Mathematics...