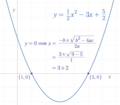
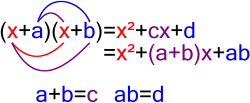In mathematics, Vieta's formulas relate the coefficients of a polynomial to sums and products of its roots. They are named after François Viète (1540-1603)...

and whose product is c (this is sometimes called "Vieta's rule" and is related to Vieta's formulas). As an example, x2 + 5x + 6 factors as (x + 3)(x +...

of Vieta jumping, all of which involve the common theme of infinite descent by finding new solutions to an equation using Vieta's formulas. Vieta jumping...

MR 2036595. Kreminski, Rick (2008). "π to thousands of digits from Vieta's formula". Mathematics Magazine. 81 (3): 201–207. doi:10.1080/0025570X.2008...

roots, which is provided by Vieta's formulas. A difference with other characteristics is that, in characteristic 2, the formula for a double root involves...

made during the late sixteenth – early 17th century.[citation needed] Vieta's formulas Michael Stifel Rafael Bombelli Cantor 1911, p. 57. Goldstein, Bernard...

named after him Vieta's formulas, expressing the coefficients of a polynomial as signed sums and products of its roots. Artūras Vieta (born 1961), Lithuanian...

identity ⁠ x 1 x 2 = c / a {\displaystyle x_{1}x_{2}=c/a} ⁠, one of Vieta's formulas. Alternately, it can be derived by dividing each side of the equation...

+ r3). This is indeed true and it follows from Vieta's formulas. It also follows from Vieta's formulas, together with the fact that we are working with...

leading coefficient and a product of monic irreducible polynomials. Vieta's formulas are simpler in the case of monic polynomials: The ith elementary symmetric...

roots of polynomials with real coefficients come in conjugate pairs. Vieta's formulas relate the coefficients of a polynomial to sums and products of its...

reducible fraction r 1 = r a . {\displaystyle r_{1}={\tfrac {r}{a}}.} By Vieta's formulas, the other root r 2 {\displaystyle r_{2}} is r 2 = − b a − r 1 = −...

and (X1, ..., Xn) an ordered list of indeterminates. According to Vieta's formulas this defines the generic monic polynomial of degree n F ( X ) = X n...

coefficients of a polynomial with roots 0, 1, ..., n − 1, one has by Vieta's formulas that [ n n − k ] = ∑ 0 ≤ i 1 < … < i k < n i 1 i 2 ⋯ i k . {\displaystyle...

and g(x) is the quadratic lower bound. By the area integral formulas above and Vieta's formula, we can obtain that A = ( b 2 − 4 a c ) 3 / 2 6 a 2 = a 6...

polynomial are called Vieta's formulas. The characteristic polynomial of a square matrix is an example of application of Vieta's formulas. The roots of this...

_{4}+\alpha _{2}\alpha _{3}){\bigr )}{\text{,}}} a fact the follows from Vieta's formulas. In other words, R4(y) is the monic polynomial whose roots are α1α2...

Rational function Partial fraction Partial fraction decomposition over R Vieta's formulas Integer-valued polynomial Algebraic equation Factor theorem Polynomial...

algebra). The coefficients of a polynomial and its roots are related by Vieta's formulas. Some polynomials, such as x2 + 1, do not have any roots among the...

(n)={\begin{cases}1,&n=1\\0,&n>1.\end{cases}}} This is an immediate consequence of Vieta's formulas. In fact, the nth roots of unity being the roots of the polynomial...

JSTOR 2308881. François Viète (1540-1603), Vieta's formulas, https://en.wikipedia.org/wiki/Vieta%27s_formulas Björck, Å.; Pereyra, V. (1970). "Solution...

permutations of the x i {\displaystyle x_{i}} induce automorphisms of H. Vieta's formulas imply that every element of K is a symmetric function of the x i ,...

a=x+y\quad {\text{and}}\quad \pm 2{\sqrt {xy}}={\sqrt {c}}.} It follows by Vieta's formulas that x and y must be roots of the quadratic equation z 2 − a z + c...

x_{n}.\end{aligned}}} These are in fact just instances of Vieta's formulas. They show that all coefficients of the polynomial are given in terms...

{\displaystyle f(z)=z^{3}+z\sum _{j}z_{j}z_{j+1}-z_{0}z_{1}z_{2}} by Vieta's formulas (for notational cleanness, we "loop back" the indices, that is, z 3...

then | b m | ≤ | a n | , {\displaystyle |b_{m}|\leq |a_{n}|,} and, by Vieta's formulas, | b i | | b m | ≤ ( m i ) M ( p ) | a n | , {\displaystyle {\frac...

\choose 3}t^{m-1}\pm \cdots +(-1)^{m}{{2m+1} \choose {2m+1}}.} By Vieta's formulas we can calculate the sum of the roots directly by examining the first...

that the inverse map that maps roots to coefficients is described by Vieta's formulas (note for characteristic polynomials that a n ≡ 1 {\displaystyle a_{n}\equiv...

terms of roots α , β , γ {\displaystyle \alpha ,\beta ,\gamma } with Vieta's formulas: σ 1 = α + β + γ = 0 σ 2 = α β + α γ + β γ = − 1 σ 3 = α β γ = 1. {\displaystyle...

theory, or from the fundamental theorem of symmetric polynomials and Vieta's formulas by noting that this expression is a symmetric polynomial in the roots...