a generating function is a representation of an infinite sequence of numbers as the coefficients of a formal power series. Generating functions are...
87 KB (14,462 words) - 22:42, 3 May 2025
In probability theory and statistics, the moment-generating function of a real-valued random variable is an alternative specification of its probability...
19 KB (2,820 words) - 18:06, 19 July 2025
Cumulant (redirect from Cumulant generating function)
are defined using the cumulant-generating function K(t), which is the natural logarithm of the moment-generating function: K ( t ) = log E [ e t X ]...
50 KB (8,877 words) - 04:04, 25 May 2025
probability generating function of a discrete random variable is a power series representation (the generating function) of the probability mass function of the...
10 KB (1,758 words) - 20:39, 26 April 2025
specifically in Hamiltonian mechanics, a generating function is, loosely, a function whose partial derivatives generate the differential equations that determine...
4 KB (354 words) - 15:10, 23 May 2025
of a sequence's generating function provides a method of converting the generating function for one sequence into a generating function enumerating another...
62 KB (11,140 words) - 00:12, 16 July 2025
an exponential function of the square root of its argument. The multiplicative inverse of its generating function is the Euler function; by Euler's pentagonal...
27 KB (4,364 words) - 02:25, 23 June 2025
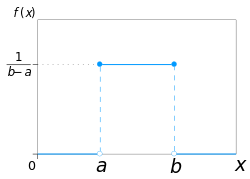
Continuous uniform distribution (redirect from Uniform density function)
would be 1 15 . {\displaystyle {\tfrac {1}{15}}.} The moment-generating function of the continuous uniform distribution is: M X = E [ e t X ] =...
28 KB (4,230 words) - 23:30, 5 April 2025
canonical. The various generating functions and its properties tabulated below is discussed in detail: The type 1 generating function G1 depends only on the...
75 KB (12,419 words) - 19:08, 30 July 2025
Binomial coefficient (redirect from Choose function)
binomial coefficients are to exponential generating series what falling factorials are to ordinary generating series. The product of all binomial coefficients...
62 KB (10,790 words) - 17:37, 29 July 2025
moment-generating function, and call the logarithm of the characteristic function the second cumulant generating function. Characteristic functions can be...
38 KB (5,208 words) - 13:53, 16 April 2025
Normal distribution (redirect from Normal density function)
\operatorname {E} [X^{k}]} . The cumulant generating function is the logarithm of the moment generating function, namely g ( t ) = ln M ( t ) = μ t + 1...
149 KB (21,749 words) - 21:46, 22 July 2025
Formula for primes (redirect from Prime generating function)
In number theory, a formula for primes is a formula generating the prime numbers, exactly and without exception. Formulas for calculating primes do exist;...
25 KB (4,183 words) - 12:09, 2 August 2025
Rodrigues' formula (section Generating function)
orthogonal polynomials obtained from the Rodrigues formula have a generating function of the form G ( x , u ) = ∑ n = 0 ∞ u n P n ( x ) G(x,u)=\sum _{n=0}^{\infty...
17 KB (3,619 words) - 11:24, 14 July 2025
}}=e^{2x}I_{0}(2x),} where I0 is a modified Bessel function of the first kind. The generating function of the squares of the central binomial coefficients...
7 KB (1,238 words) - 17:35, 23 November 2024
Hermite polynomials (redirect from Hermite function)
expansion at x of the entire function z → e−z2 (in the physicist's case). One can also derive the (physicist's) generating function by using Cauchy's integral...
73 KB (13,245 words) - 14:43, 1 August 2025
functional equation is satisfied by the generating function of any rational cone (defined below) and the generating function of the cone's interior. A rational...
2 KB (333 words) - 07:37, 8 July 2024
and statistics, a probability mass function (sometimes called probability function or frequency function) is a function that gives the probability that a...
10 KB (1,539 words) - 19:51, 12 March 2025
Meijer G-function. The characteristic function has also been obtained by Muraleedharan et al. (2007). The characteristic function and moment generating function...
42 KB (6,123 words) - 19:09, 27 July 2025
enumeration, and frequently involves deriving a recurrence relation or generating function and using this to arrive at the desired closed form. Often, a complicated...
10 KB (1,360 words) - 05:16, 9 December 2024
the constant of proportionality is 1. This function is closely related to the exponential generating function of the Hermite polynomials, which are the...
17 KB (2,039 words) - 15:09, 3 March 2024
calculate the generating function F ( x ) = ∑ n ≥ 0 H ( n ) x n {\displaystyle F(x)=\sum _{n\geq 0}H(n)x^{n}} . The generating function satisfies F (...
9 KB (728 words) - 14:40, 18 January 2025
Binomial transform (category Hypergeometric functions)
binomial transform to the sequence associated with its ordinary generating function. The binomial transform, T, of a sequence, {an}, is the sequence...
14 KB (2,438 words) - 15:02, 19 April 2025
roots of the first few spherical Bessel functions are: The spherical Bessel functions have the generating functions 1 z cos ( z 2 − 2 z t ) = ∑ n = 0 ∞...
77 KB (12,329 words) - 12:54, 29 July 2025
{\displaystyle M_{\pi }} is the moment generating function of the density. For the probability generating function, one obtains m X ( s ) = M π ( s − 1...
10 KB (1,169 words) - 10:24, 10 June 2025
Fibonacci sequence (section Generating function)
its conjugate. The related function z ↦ − s ( − 1 / z ) {\textstyle z\mapsto -s\left(-1/z\right)} is the generating function for the negafibonacci numbers...
85 KB (12,946 words) - 22:47, 28 July 2025
Spherical harmonics (redirect from Spheroidal function)
and λ {\displaystyle \lambda } as real parameters. In naming this generating function after Herglotz, we follow Courant & Hilbert 1962, §VII.7, who credit...
75 KB (12,488 words) - 23:57, 29 July 2025
{\displaystyle n\geq 0} these weighted harmonic number expansions are generated by the generating function 1 n ! [ n + 1 k ] = [ x k ] exp ( ∑ m ≥ 1 ( − 1 ) m − 1...
38 KB (7,265 words) - 04:38, 9 June 2025
confluent hypergeometric function and J1 is the Bessel function of the first kind. Likewise the moment generating function can be calculated as M ( t...
8 KB (988 words) - 04:16, 7 July 2025
of F generated by the coordinates of P. The logarithmic derivative of the infinite product Z(X, t) is easily seen to be the generating function discussed...
9 KB (1,449 words) - 00:25, 10 February 2025