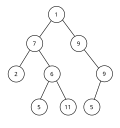
In graph theory, an arborescence is a directed graph where there exists a vertex r (called the root) such that, for any other vertex v, there is exactly...

up arborescence in Wiktionary, the free dictionary. Arborescence refers to any tree-like structure. It may also refer to: Arborescence (graph theory) Arborescence...

In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed...

In graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one path, or equivalently a connected acyclic undirected...

Mutualism Perspectivism Plane of immanence Graph (abstract data type) Arborescence (graph theory) Tree (graph theory) Digital infinity Intertwingularity Young...

In mathematics, and, in particular, in graph theory, a rooted graph is a graph in which one vertex has been distinguished as the root. Both directed and...

Appendix:Glossary of graph theory in Wiktionary, the free dictionary. This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes...

In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it...

In graph theory, an Eulerian trail (or Eulerian path) is a trail in a finite graph that visits every edge exactly once (allowing for revisiting vertices)...

The theory of random graphs lies at the intersection between graph theory and probability theory. From a mathematical perspective, random graphs are used...

From a graph theory perspective, binary trees as defined here are arborescences. A binary tree may thus be also called a bifurcating arborescence, a term...

In combinatorics and order theory, a multitree may describe either of two equivalent structures: a directed acyclic graph (DAG) in which there is at most...

of graph theory, a spanning tree T of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G. In general, a graph may...

direction (a more narrow term is an "arborescence"), meaning: A directed graph, whose underlying undirected graph is a tree (any two vertices are connected...

undirected graph that is acyclic. A polytree is an example of an oriented graph. The term polytree was coined in 1987 by Rebane and Pearl. An arborescence is...

graph theory, a connected graph is k-edge-connected if it remains connected whenever fewer than k edges are removed. The edge-connectivity of a graph...

In graph theory, Edmonds' algorithm or Chu–Liu/Edmonds' algorithm is an algorithm for finding a spanning arborescence of minimum weight (sometimes called...

In graph theory, a part of discrete mathematics, the BEST theorem gives a product formula for the number of Eulerian circuits in directed (oriented) graphs...

can also be modelled as finding a maximum-probability spanning arborescence over the graph of all possible dependency edges, and then picking dependency...

In graph theory, an m-ary tree (for nonnegative integers m) (also known as n-ary, k-ary, k-way or generic tree) is an arborescence (or, for some authors...

in this context are directed graphs, oriented from the root towards the leaves; in other words, they are arborescences. The degree of a node in a tree...

minimum spanning tree is NP-hard in general. An arborescence is a variant of MST for directed graphs. It can be solved in O ( E + V log ⁡ V ) {\displaystyle...

Apostolico–Giancarlo algorithm approximate string matching approximation algorithm arborescence arithmetic coding array array index array merging array search articulation...

l − k ) {\displaystyle (k,l-k)} -arborescence; this was first shown for ( 2 , 3 ) {\displaystyle (2,3)} sparse graphs. Additionally, many of the rigidity...

adjacency list versus adjacency matrix for graphs) is irrelevant, because species are purely algebraic. Category theory provides a useful language for the concepts...

tree or arborescence that is formed by a stochastic process. Types of random trees include: Uniform spanning tree, a spanning tree of a given graph in which...

matchings and maximum weight matchings in bipartite graphs and finding arborescences in directed graphs. The matroid intersection theorem, due to Jack Edmonds...

{\displaystyle n} -vertex arborescence. Rosenfeld (1972) conjectured that every orientation of an n {\displaystyle n} -vertex path graph (with n ≥ 8 {\displaystyle...

trained as an architect, so some of his drawings, which he called 'arborescences', resembled both organic forms and architectural structures." These...

events, corresponds to an "anti-arborescence", contrary to the "arborescent stories" that, in accordance to graph theory, seek to bifurcate events as much...