algebra, Berlekamp's algorithm is a well-known method for factoring polynomials over finite fields (also known as Galois fields). The algorithm consists...

The Berlekamp–Massey algorithm is an algorithm that will find the shortest linear-feedback shift register (LFSR) for a given binary output sequence. The...

the preceding algorithm, this algorithm uses the same subalgebra B of R as the Berlekamp's algorithm, sometimes called the "Berlekamp subagebra" and...

Berkeley. Berlekamp was widely known for his work in computer science, coding theory and combinatorial game theory. Berlekamp invented an algorithm to factor...

The Berlekamp–Welch algorithm, also known as the Welch–Berlekamp algorithm, is named for Elwyn R. Berlekamp and Lloyd R. Welch. This is a decoder algorithm...

In number theory, Berlekamp's root finding algorithm, also called the Berlekamp–Rabin algorithm, is the probabilistic method of finding roots of polynomials...

time needed to choose the right subsets of mod p factors. Berlekamp's algorithm Berlekamp, E. R. (1967), "Factoring polynomials over finite fields",...

The Reeds–Sloane algorithm, named after James Reeds and Neil Sloane, is an extension of the Berlekamp–Massey algorithm, an algorithm for finding the shortest...

modulo a prime number Berlekamp's root finding algorithm Cipolla's algorithm Tonelli–Shanks algorithm Multiplication algorithms: fast multiplication of...

1981. It is arguably the dominant algorithm for solving the problem, having replaced the earlier Berlekamp's algorithm of 1967. It is currently implemented...

The Tonelli–Shanks algorithm (referred to by Shanks as the RESSOL algorithm) is used in modular arithmetic to solve for r in a congruence of the form r2...

A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic or procedure. The algorithm typically uses uniformly random...

Gosper's algorithm Limit computation via e.g. Gruntz's algorithm Polynomial factorization via e.g., over finite fields, Berlekamp's algorithm or Cantor–Zassenhaus...

Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor...

The Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen...

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers...

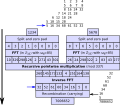
The Karatsuba algorithm is a fast multiplication algorithm for integers. It was discovered by Anatoly Karatsuba in 1960 and published in 1962. It is a...

co-inventor of the Baum–Welch algorithm and the Berlekamp–Welch algorithm, also known as the Welch–Berlekamp algorithm. Welch received his B.S. in mathematics...

The binary GCD algorithm, also known as Stein's algorithm or the binary Euclidean algorithm, is an algorithm that computes the greatest common divisor...

theory, the Pohlig–Hellman algorithm, sometimes credited as the Silver–Pohlig–Hellman algorithm, is a special-purpose algorithm for computing discrete logarithms...

and computer programming, the extended Euclidean algorithm is an extension to the Euclidean algorithm, and computes, in addition to the greatest common...

multiplication algorithm is an algorithm (or method) to multiply two numbers. Depending on the size of the numbers, different algorithms are more efficient...

Pollard's p − 1 algorithm is a number theoretic integer factorization algorithm, invented by John Pollard in 1974. It is a special-purpose algorithm, meaning...

In computational number theory, the index calculus algorithm is a probabilistic algorithm for computing discrete logarithms. Dedicated to the discrete...

theory, Williams's p + 1 algorithm is an integer factorization algorithm, one of the family of algebraic-group factorisation algorithms. It was invented by...

Pollard's rho algorithm is an algorithm for integer factorization. It was invented by John Pollard in 1975. It uses only a small amount of space, and...

Schoof's algorithm is an efficient algorithm to count points on elliptic curves over finite fields. The algorithm has applications in elliptic curve cryptography...

efficient non-quantum integer factorization algorithm is known. However, it has not been proven that such an algorithm does not exist. The presumed difficulty...

Lenstra–Lenstra–Lovász (LLL) lattice basis reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and...

Pollard's rho algorithm for logarithms is an algorithm introduced by John Pollard in 1978 to solve the discrete logarithm problem, analogous to Pollard's...