In mathematics, the Cantor function is an example of a function that is continuous, but not absolutely continuous. It is a notorious counterexample in...
21 KB (3,497 words) - 21:39, 11 July 2025
pairing function can also be generalized: there exists an n-ary generalized Cantor pairing function on N {\displaystyle \mathbb {N} } . The Cantor pairing...
15 KB (2,488 words) - 13:28, 9 August 2025
The Cantor distribution is the probability distribution whose cumulative distribution function is the Cantor function. This distribution has neither a...
6 KB (811 words) - 18:39, 10 November 2023
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874...
42 KB (6,396 words) - 00:29, 17 July 2025
Cantor's diagonal argument (among various similar names) is a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence...
28 KB (2,808 words) - 11:08, 29 June 2025
mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it...
5 KB (662 words) - 19:46, 30 July 2025
Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6...
85 KB (10,164 words) - 06:38, 2 August 2025
Schröder–Bernstein theorem (redirect from Cantor-Schroeder-Berntein theorem)
Schröder. It is also known as the Cantor–Bernstein theorem or Cantor–Schröder–Bernstein theorem, after Georg Cantor, who first published it (albeit without...
20 KB (2,377 words) - 11:57, 23 March 2025
see Cantor function. if this set is countable, then f {\displaystyle f} is absolutely continuous if f {\displaystyle f} is a monotonic function defined...
19 KB (2,475 words) - 06:23, 2 July 2025
of a singular function is the Cantor function, which is sometimes called the devil's staircase (a term also used for singular functions in general). There...
4 KB (416 words) - 14:40, 9 October 2024
Uniform continuity (redirect from Uniformly continuous function)
Any absolutely continuous function (over a compact interval) is uniformly continuous. On the other hand, the Cantor function is uniformly continuous but...
25 KB (4,170 words) - 00:42, 30 June 2025
normal. The Cantor set is also null. Thus, almost all reals are not in it even though it is uncountable. The derivative of the Cantor function is 0 for almost...
25 KB (2,577 words) - 23:35, 18 April 2024
Space-filling curve (redirect from Space filling function)
(The restriction of the Cantor function to the Cantor set is an example of such a function.) From it, we get a continuous function H {\displaystyle H} from...
16 KB (1,971 words) - 03:58, 9 July 2025
Absolute continuity (redirect from Absolutely continuous function)
example with the Cantor function. Let I {\displaystyle I} be an interval in the real line R {\displaystyle \mathbb {R} } . A function f : I → R {\displaystyle...
19 KB (2,686 words) - 18:05, 4 August 2025
In mathematics, the Smith–Volterra–Cantor set (SVC), ε-Cantor set, or fat Cantor set is an example of a set of points on the real line that is nowhere...
6 KB (966 words) - 13:10, 12 July 2025
Pathological (mathematics) (redirect from Pathological function)
Dirichlet function, which is the indicator function for rationals, is a bounded function that is not Riemann integrable. The Cantor function is a monotonic...
19 KB (2,392 words) - 12:14, 18 July 2025
cumulative distribution function g is continuous, it does not work if g fails to be absolutely continuous (again, the Cantor function may serve as an example...
19 KB (2,816 words) - 23:59, 12 July 2025
well-known fractal curves, including the Cantor function, Cesàro–Faber curve (Lévy C curve), Minkowski's question mark function, blancmange curve, and the Koch...
15 KB (2,813 words) - 00:24, 8 November 2024
Apollonian gasket Attractor Box-counting dimension Cantor distribution Cantor dust Cantor function Cantor set Cantor space Chaos theory Coastline Constructal theory...
1 KB (144 words) - 15:51, 20 July 2024
Cantor Set and Cantor Function". Mathematics Magazine. 67 (2): 136–140. doi:10.1080/0025570X.1994.11996201 – via Taylor and Francis+NEJM. The Cantor Set...
17 KB (1,925 words) - 19:01, 5 October 2024
X} to Y {\displaystyle Y} . This is the heart of Cantor's theorem: there is no surjective function from any set A {\displaystyle A} to its power set...
22 KB (3,735 words) - 00:55, 8 December 2024
Cantor distribution Cantor function Cantor medal, German mathematics prize named after Georg Cantor Cantor set Cantor space Cantor's theorem (disambiguation)...
1 KB (202 words) - 22:48, 7 May 2025
Riemann-integrable. The function is defined by making use of the Smith–Volterra–Cantor set and an infinite number or "copies" of sections of the function defined by...
5 KB (587 words) - 21:22, 16 November 2024
may fail for continuous functions F that admit a derivative f(x) at almost every point x, as the example of the Cantor function shows. However, if F is...
31 KB (4,883 words) - 05:40, 13 July 2025
Bounded variation (redirect from Function variation)
V_{a}^{b}(f)=|f(b)-f(a)|.} In particular, the monotone Cantor function is a well-known example of a function of bounded variation that is not absolutely continuous...
61 KB (8,441 words) - 20:55, 29 April 2025
theorem still fails. As an example, take F {\displaystyle F} to be the Cantor function and again let G = 0. {\displaystyle G=0.} It turns out that adding...
9 KB (1,608 words) - 02:59, 18 July 2025
a nonmeasurable subset. Let f {\displaystyle f} be the Cantor function, a continuous function which is locally constant on K c , {\displaystyle K^{c}...
11 KB (1,735 words) - 17:01, 11 July 2025
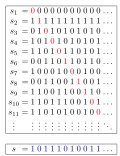
147. Cantor function, which can be understood as reinterpreting ternary numbers as binary numbers, analogously to the way the question-mark function reinterprets...
26 KB (3,855 words) - 00:18, 5 August 2025
Hölder condition (redirect from Hölder continuous function)
continuous by the Heine-Cantor theorem. It does not satisfy a Hölder condition of any order, however. The Weierstrass function defined by: f ( x ) = ∑...
14 KB (2,415 words) - 13:28, 8 March 2025
Uniformly connected space (redirect from Cantor connectendess)
uniformly connected space or Cantor connected space is a uniform space U such that every uniformly continuous function from U to a discrete uniform space...
944 bytes (97 words) - 05:20, 27 December 2018