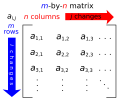
In mathematics, a Cauchy matrix, named after Augustin-Louis Cauchy, is an m×n matrix with elements aij in the form a i j = 1 x i − y j ; x i − y j ≠ 0...

Hankel matrix that needs to be inverted in order to obtain the weight parameters of the polynomial distribution approximation. Cauchy matrix Jacobi operator...

the field of complex analysis in mathematics, the Cauchy–Riemann equations, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two...

The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is an upper bound on the absolute value of the inner product between...

submatrix is positive). The Hilbert matrix is an example of a Hankel matrix. It is also a specific example of a Cauchy matrix. The determinant can be expressed...

Baron Augustin-Louis Cauchy FRS FRSE (UK: /ˈkoʊʃi/ KOH-shee, /ˈkaʊʃi / KOW-shee, US: /koʊˈʃiː / koh-SHEE; French: [oɡystɛ̃ lwi koʃi]; 21 August 1789 –...

notions, including the remark that, in modern parlance, matrix products are non-commutative. Cauchy was the first to prove general statements about determinants...

The Cauchy distribution, named after Augustin-Louis Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as...

theorem Cauchy matrix (and Cauchy determinant) Cauchy net Cauchy–Peano theorem Cauchy point Cauchy principal value Cauchy problem Abstract Cauchy problem...

transpose of a matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix A by producing...

continuum mechanics, the Cauchy stress tensor (symbol σ {\displaystyle {\boldsymbol {\sigma }}} , named after Augustin-Louis Cauchy), also called true stress...

matrix whose columns are the columns of A at indices from S, and BS,[m] for the m×m matrix whose rows are the rows of B at indices from S. The Cauchy–Binet...

such norms are referred to as matrix norms. Matrix norms differ from vector norms in that they must also interact with matrix multiplication. Given a field...

criterion for more details. Both the formula for ordinary matrix multiplication and the Cauchy–Binet formula for the determinant of the product of two matrices...

using an FPGA. The above Vandermonde matrix solution can be extended to triple parity, but for beyond a Cauchy matrix construction is required. The following...

2n\times 2n} matrix. As the object of study in several complex variables are holomorphic functions, that is, solutions to the n-dimensional Cauchy–Riemann...

classical adjoint of a square matrix A, adj(A), is the transpose of its cofactor matrix. It is occasionally known as adjunct matrix, or "adjoint", though that...

principal axes are the eigenvectors of the inertia matrix. In the early 19th century, Augustin-Louis Cauchy saw how their work could be used to classify the...

In algebra, the Binet–Cauchy identity, named after Jacques Philippe Marie Binet and Augustin-Louis Cauchy, states that ( ∑ i = 1 n a i c i ) ( ∑ j = 1...

matrices used in mathematics, science and engineering. A matrix (plural matrices, or less commonly matrixes) is a rectangular array of numbers called entries...

square matrix. The determinant of a matrix A is commonly denoted det(A), det A, or |A|. Its value characterizes some properties of the matrix and the...

respect to any chosen coordinate system, the Cauchy stress tensor can be represented as a symmetric matrix of 3×3 real numbers. Even within a homogeneous...

vector calculus, the Jacobian matrix (/dʒəˈkoʊbiən/, /dʒɪ-, jɪ-/) of a vector-valued function of several variables is the matrix of all its first-order partial...

A singular matrix is a square matrix that is not invertible, unlike non-singular matrix which is invertible. Equivalently, an n {\displaystyle n} -by-...

on "Kantorovich inequality" Marshall, A. W. and Olkin, I., Matrix versions of the Cauchy and Kantorovich inequalities. Aequationes Mathematicae 40 (1990)...

In mathematics, the Cauchy–Kovalevskaya theorem (also written as the Cauchy–Kowalevski theorem) is the main local existence and uniqueness theorem for...

value theorem in its modern form was stated and proved by Augustin Louis Cauchy in 1823. Many variations of this theorem have been proved since then. Let...

In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices. It collects the various...

incidence matrix and its transpose, i.e., L = EET. Furthermore, let F be the matrix E with its first row deleted, so that FFT = M11. Now the Cauchy–Binet...

In linear algebra, the trace of a square matrix A, denoted tr(A), is the sum of the elements on its main diagonal, a 11 + a 22 + ⋯ + a n n {\displaystyle...