In mathematics, compact objects, also referred to as finitely presented objects, or objects of finite presentation, are objects in a category satisfying...

A mathematical object is an abstract concept arising in mathematics. Typically, a mathematical object can be a value that can be assigned to a symbol...

In mathematics, specifically in category theory, an exponential object or map object is the categorical generalization of a function space in set theory...

In mathematics, an invariant is a property of a mathematical object (or a class of mathematical objects) which remains unchanged after operations or transformations...

category theory, a branch of mathematics, a dual object is an analogue of a dual vector space from linear algebra for objects in arbitrary monoidal categories...

formulas: expressions are a kind of mathematical object, whereas formulas are statements about mathematical objects. This is analogous to natural language...

In mathematics, a characterization of an object is a set of conditions that, while possibly different from the definition of the object, is logically equivalent...

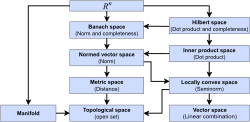
define the notion of "space" itself. A space consists of selected mathematical objects that are treated as points, and selected relationships between these...

In mathematics, the ind-completion or ind-construction is the process of freely adding filtered colimits to a given category C. The objects in this ind-completed...

canonical A reference to a standard or choice-free presentation of some mathematical object (e.g., canonical map, canonical form, or canonical ordering). The...

location', and λόγος, 'study') is the branch of mathematics concerned with the properties of a geometric object that are preserved under continuous deformations...

every area of mathematics". Many mathematical dualities between objects of two types correspond to pairings, bilinear functions from an object of one type...

paracompactifying. Bounded function – A mathematical function the set of whose values is bounded Bump function – Smooth and compactly supported function Support of...

In mathematics, algebraically compact modules, also called pure-injective modules, are modules that have a certain "nice" property which allows the solution...

In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...

(and those in related sciences) very frequently speak of whether a mathematical object—a function, a set, a space of one sort or another—is "well-behaved"...

(TV series), a 1960s British soap opera Compact star, also called a compact object, a degenerate star like a neutron star Campact, a German nongovernmental...

In mathematics and logic, the term "uniqueness" refers to the property of being the one and only object satisfying a certain condition. This sort of quantification...

In mathematics, a classification theorem answers the classification problem: "What are the objects of a given type, up to some equivalence?". It gives...

In mathematics, Pontryagin duality is a duality between locally compact abelian groups that allows generalizing Fourier transform to all such groups, which...

Mathematics is a broad subject that is commonly divided in many areas or branches that may be defined by their objects of study, by the used methods, or...

In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical...

integers, together with the operation ⁠ + {\displaystyle +} ⁠, form a mathematical object belonging to a broad class sharing similar structural aspects. To...

\colon F\to M} is the required surjection. The projective objects in the category of compact Hausdorff spaces are precisely the extremally disconnected...

In mathematics, a set is a collection of different things; the things are elements or members of the set and are typically mathematical objects: numbers...

The field of mathematics that studies sheaves is called sheaf theory. Sheaves are understood conceptually as general and abstract objects. Their precise...

In mathematics, a matrix (pl.: matrices) is a rectangular array or table of numbers or other mathematical objects with elements or entries arranged in...

In mathematics, a *-autonomous (read "star-autonomous") category C is a symmetric monoidal closed category equipped with a dualizing object ⊥ {\displaystyle...

Mathematical logic is the study of formal logic within mathematics. Major subareas include model theory, proof theory, set theory, and recursion theory...

whether or not mathematical objects are purely abstract entities or are in some way concrete, and in what the relationship such objects have with physical...