In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal x-axis, called...
32 KB (4,586 words) - 14:31, 13 July 2025
in adding more structure, one may view the plane as a 1-dimensional complex manifold, called the complex line. Many fundamental tasks in mathematics...
7 KB (1,672 words) - 16:13, 9 June 2025
Riemann sphere (redirect from Extended complex plane)
of the extended complex plane (also called the closed complex plane): the complex plane plus one point at infinity. This extended plane represents the...
22 KB (3,390 words) - 08:33, 1 July 2025
standard basis makes the complex numbers a Cartesian plane, called the complex plane. This allows a geometric interpretation of the complex numbers and their...
91 KB (12,021 words) - 17:33, 29 May 2025
Holomorphic function (redirect from Complex differentiable)
regular functions. A holomorphic function whose domain is the whole complex plane is called an entire function. The phrase "holomorphic at a point z...
25 KB (3,490 words) - 21:26, 15 June 2025
Poincaré half-plane model. Mathematicians sometimes identify the Cartesian plane with the complex plane, and then the upper half-plane corresponds to...
6 KB (1,033 words) - 17:49, 19 June 2025
These logarithms are equally spaced along a vertical line in the complex plane. A complex-valued function log : U → C {\displaystyle \log \colon U\to \mathbb...
30 KB (4,831 words) - 04:18, 11 July 2025
In mathematics, the complex projective plane, usually denoted P 2 ( C ) {\displaystyle \mathbb {P} ^{2}(\mathbb {C} )} or C P 2 , {\displaystyle...
3 KB (527 words) - 02:57, 10 November 2024
complex ones. The hyperbolic unit j is not a real number but an independent quantity. The collection of all such z is called the split-complex plane....
28 KB (4,144 words) - 22:10, 6 July 2025
getting a complex analytic function whose domain is the whole complex plane with a finite number of curve arcs removed. Many basic and special complex functions...
18 KB (2,538 words) - 09:09, 12 May 2025
Phasor (redirect from Complex amplitude)
A\cos(\omega t+\theta ).} Figure 2 depicts it as a rotating vector in the complex plane. It is sometimes convenient to refer to the entire function as a phasor...
31 KB (4,997 words) - 10:09, 1 July 2025
represent physical positions, like an affine plane or complex plane. The most basic example is the flat Euclidean plane, an idealization of a flat surface in...
7 KB (803 words) - 22:02, 19 August 2024
Unit circle (section In the complex plane)
additional examples. In the complex plane, numbers of unit magnitude are called the unit complex numbers. This is the set of complex numbers z such that | z...
8 KB (1,009 words) - 18:06, 10 March 2025
In mathematics, a plane curve is a curve in a plane that may be a Euclidean plane, an affine plane or a projective plane. The most frequently studied cases...
5 KB (670 words) - 00:49, 20 April 2024
Sine and cosine (redirect from Complex sine and cosine)
the complex plane, the function e i x {\displaystyle e^{ix}} for real values of x {\displaystyle x} traces out the unit circle in the complex plane. Both...
55 KB (7,064 words) - 00:33, 30 May 2025
Zeros and poles (redirect from Zero (complex analysis))
meromorphic functions. For example, if a function is meromorphic on the whole complex plane plus the point at infinity, then the sum of the multiplicities of its...
9 KB (1,479 words) - 11:37, 3 May 2025
In the mathematical field of complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all...
9 KB (1,215 words) - 15:05, 13 July 2025
thought of as deformed versions of the complex plane: locally near every point they look like patches of the complex plane, but the global topology can be quite...
26 KB (3,142 words) - 10:43, 20 March 2025
Exponential function (redirect from Complex exponential function)
generalized to accept complex numbers as arguments. This reveals relations between multiplication of complex numbers, rotations in the complex plane, and trigonometry...
37 KB (5,079 words) - 14:15, 7 July 2025
Absolute value (redirect from Modulus of complex number)
The absolute value of a complex number is defined by the Euclidean distance of its corresponding point in the complex plane from the origin. This can...
28 KB (3,500 words) - 06:29, 17 July 2025
Generalised circle (section Extended complex plane)
sphere. The extended Euclidean plane can be identified with the extended complex plane, so that equations of complex numbers can be used to describe...
7 KB (1,131 words) - 23:27, 28 December 2023
Infinity (redirect from Complex infinity)
\infty } can be added to the complex plane as a topological space giving the one-point compactification of the complex plane. When this is done, the resulting...
54 KB (6,115 words) - 01:14, 15 July 2025
a complex contour integral which is path-independent because exp ( − t 2 ) {\displaystyle \exp(-t^{2})} is holomorphic on the whole complex plane C...
48 KB (7,358 words) - 08:30, 16 July 2025
Extrapolation (section In the complex plane)
This transform exchanges the part of the complex plane inside the unit circle with the part of the complex plane outside of the unit circle. In particular...
13 KB (1,701 words) - 03:36, 2 June 2025
Euler's formula (redirect from Eulers formula in complex analysis)
ex to the complex plane. The exponential function f ( z ) = e z {\displaystyle f(z)=e^{z}} is the unique differentiable function of a complex variable...
27 KB (3,946 words) - 09:55, 16 July 2025
Gamma function (redirect from Complex number factorial)
d}}t,\ \qquad \Re (z)>0\,.} The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic...
90 KB (13,547 words) - 17:59, 24 June 2025
method can also be applied to complex functions to find their roots. Each root has a basin of attraction in the complex plane; these basins can be mapped...
34 KB (3,755 words) - 10:08, 5 July 2025
triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers...
14 KB (1,896 words) - 08:34, 5 May 2025
definition of a complex analytic function is obtained by replacing, in the definitions above, "real" with "complex" and "real line" with "complex plane". A function...
15 KB (2,233 words) - 20:17, 16 July 2025
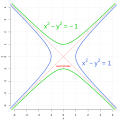
Unit hyperbola (section Complex plane algebra)
geometry, the unit hyperbola is the set of points (x,y) in the Cartesian plane that satisfy the implicit equation x 2 − y 2 = 1. {\displaystyle x^{2}-y^{2}=1...
10 KB (1,507 words) - 07:45, 24 April 2025