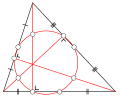
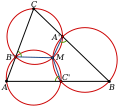
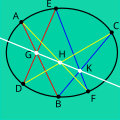
geometry, a set of points are said to be concyclic (or cocyclic) if they lie on a common circle. A polygon whose vertices are concyclic is called a cyclic...

because it passes through nine significant concyclic points defined from the triangle. These nine points are: The midpoint of each side of the triangle...

can be circumscribed by a circle. The vertices of this polygon are concyclic points. All triangles are cyclic polygons. Cyclic quadrilateral, a special...

distances determined by four points in the plane or in a higher-dimensional space. It states that, for any four points A, B, C, and D, the following...

line segments joining the object points with their image points are all concurrent at the optical centre. Concyclic points Coplanarity Direction (geometry)...

applied to the segment AF, the points ARBF are concyclic (they lie on a circle). Similarly, the points AFCQ are concyclic. ∠ARB = 60°, so ∠AFB = 120°, using...

lie on a common circle (the circumscribed circle); i.e., they are concyclic points. That is, a regular polygon is a cyclic polygon. Together with the...

because it passes through nine significant concyclic points defined from the triangle. These nine points are: The midpoint of each side of the triangle...

midpoints of the sides and the feet of the four maltitudes are eight concyclic points; the eight point circle. The center of this circle is the centroid...

the circumcenter, the Lemoine point, and the first two Brocard points are concyclic—they all fall on the same circle, of which the segment connecting...

Most of the other results discussed in the paper pertained to various concyclic points that could be constructed from the Lemoine point. Lemoine served in...

{3}{2}}G_{A}.} Thus the two centroids and the incenter are collinear. Concyclic points Tom M. Apostol and Mamikon A. Mnatsakanian (December 2004). "Figures...

common centrePages displaying short descriptions of redirect targets Concyclic – Points on a common circlePages displaying short descriptions of redirect...

 186. Ternullo, Maurizio (2009). "Two new sets of ellipse related concyclic points". Journal of Geometry. 94 (1–2): 159–173. doi:10.1007/s00022-009-0005-7...

circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and...

}&b_{3}&c_{3}\end{matrix}}\right|=0.} Menelaus theorem Ceva's theorem Concyclic Hopcroft's problem of finding point–line incidences Incidence matrix Incidence...

the new points M,N,P,R and Q are concyclic (lie on a circle). See diagram. The converse result is known as the Five circles theorem. Given points, A, B...

mid-points of the quadrilateral diagonals and the mid-points of the Van Aubel segments are concyclic. A few extensions of the theorem, considering similar...

i<j,} are concyclic (contained in a cycle) on at least four cycles c i j {\displaystyle c_{ij}} , then the sixth quadruple is also concyclic. The bundle...

triangles by its two diagonals, then the incenters of the four triangles are concyclic if and only if the quadrilateral is tangential. In fact, the incenters...

theorem Isotomic conjugate Isotomic lines Jacobi point Japanese theorem for concyclic polygons Johnson circles Kepler triangle Kobon triangle problem Kosnita's...

{OI}}={\sqrt {R(R-2r)}}.} A set of points lying on the same circle are called concyclic, and a polygon whose vertices are concyclic is called a cyclic polygon...

to show that X = AB ∩ DE, Y = BC ∩ EF, Z = CD ∩ FA are collinear for concyclic ABCDEF, then notice that △EYB and △CYF are similar, and that X and Z will...

that the points in 5 faces correspond to concyclical quadruples, then the sixth quadruple of points is concyclical, too. The converse is true, too. Theorem...

cyclic quadrilateral (that is, the four intersection points of adjacent angle bisectors are concyclic), or they are concurrent. In the latter case the quadrilateral...

quadrilateral: p.127  (that is, the four intersection points of adjacent angle bisectors are concyclic) or they are concurrent. In the latter case the quadrilateral...

Circumcircle Concyclic Incircle and excircles of a triangle Orthocentric system Monge's theorem Power center Nine-point circle Circle points segments proof...

z_{4}).\ } The cross-ratio is real if and only if the four points are either collinear or concyclic, reflecting the fact that every Möbius transformation maps...

C_{1}B_{1}C_{2}=(2n-1)C-(n-1)\pi ,} then A1, A2, B1, B2, C1 and C2 are concyclic. Sine-triple-angle circle is the special case in n=2. Also, | A 1 A 2...

(projective geometry) Japanese theorem for concyclic polygons (Euclidean geometry) Japanese theorem for concyclic quadrilaterals (Euclidean geometry) Kawasaki's...